|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The variables that determine alveolar gas tension have been described. The following additional factors also determine the gas tensions in arterial blood:
To understand fully the role of V̇A/![]() in determining arterial gas tensions, it is necessary to discard the homogeneous
lung model and consider a model with multiple parallel units of gas exchange and
blood flow in which the resulting arterial gas tension is determined by the mixing
of different proportions of blood from each gas exchange unit. The gas tensions
in each unit depend on the regional ventilation, perfusion, and diffusion.
in determining arterial gas tensions, it is necessary to discard the homogeneous
lung model and consider a model with multiple parallel units of gas exchange and
blood flow in which the resulting arterial gas tension is determined by the mixing
of different proportions of blood from each gas exchange unit. The gas tensions
in each unit depend on the regional ventilation, perfusion, and diffusion.
Gas exchange units with low or zero V̇A/![]() ratios have low end-capillary PO2
. The
O2
-blood dissociation curve has a plateau at the point at which hemoglobin
is fully saturated (see Fig. 36-9
),
and there is a maximum to which gas exchange units with normal ventilation and perfusion
can raise the end-capillary O2
content. Arterial O2
content
(and therefore PO2
) is a flow weighted
average of all gas exchange units. Under usual conditions, V̇A/
ratios have low end-capillary PO2
. The
O2
-blood dissociation curve has a plateau at the point at which hemoglobin
is fully saturated (see Fig. 36-9
),
and there is a maximum to which gas exchange units with normal ventilation and perfusion
can raise the end-capillary O2
content. Arterial O2
content
(and therefore PO2
) is a flow weighted
average of all gas exchange units. Under usual conditions, V̇A/![]() mismatching always results in arterial hypoxemia. The only circumstance in which
V̇A/
mismatching always results in arterial hypoxemia. The only circumstance in which
V̇A/![]() mismatch results in increased arterial
PO2
is during the uptake of nitrous oxide.
mismatch results in increased arterial
PO2
is during the uptake of nitrous oxide.
The effect of V̇A/![]() mismatching
on PaCO2
is often erroneously assumed
to be negligible because PaCO2
can usually
be maintained within the normal range, even in the face of severe pulmonary pathology.
This is true because the CO2
-blood dissociation curve ( Fig.
36-2
) is a monotonically increasing one. Moreover, the degree to which
end-capillary PCO2
(Pc'CO2
)
can be increased by gas exchange units with abnormal V̇A/
mismatching
on PaCO2
is often erroneously assumed
to be negligible because PaCO2
can usually
be maintained within the normal range, even in the face of severe pulmonary pathology.
This is true because the CO2
-blood dissociation curve ( Fig.
36-2
) is a monotonically increasing one. Moreover, the degree to which
end-capillary PCO2
(Pc'CO2
)
can be increased by gas exchange units with abnormal V̇A/![]() is relatively small. The venoarterial PCO2
difference is usually only 5 mm Hg under resting conditions and rarely exceeds 10
mm Hg. It is therefore usually possible for lung units with low PACO2
(and therefore
is relatively small. The venoarterial PCO2
difference is usually only 5 mm Hg under resting conditions and rarely exceeds 10
mm Hg. It is therefore usually possible for lung units with low PACO2
(and therefore
 Figure 36-2
Carbon dioxide (CO2
) content of arterial blood
as a function of PCO2
. For a given PCO2
deoxygenated blood has a higher CO2
content than oxygenated blood (i.e.,
Haldane effect). Unlike the HbO2
saturation curve, the CO2
content curve has no plateau and can be approximated by a straight line in the clinically
useful range. (Data from Christiansen J, Douglas CG, Haldane JS: The absorption
and dissociation of carbon dioxide by human blood. J Physiol [Lond] 48:244, 1914.)
Figure 36-2
Carbon dioxide (CO2
) content of arterial blood
as a function of PCO2
. For a given PCO2
deoxygenated blood has a higher CO2
content than oxygenated blood (i.e.,
Haldane effect). Unlike the HbO2
saturation curve, the CO2
content curve has no plateau and can be approximated by a straight line in the clinically
useful range. (Data from Christiansen J, Douglas CG, Haldane JS: The absorption
and dissociation of carbon dioxide by human blood. J Physiol [Lond] 48:244, 1914.)
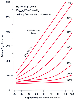 Figure 36-3
Arterial PO2
as a function of FIO2
and shunt fraction
(
Figure 36-3
Arterial PO2
as a function of FIO2
and shunt fraction
(![]() S/
S/![]() T).
Assumptions are shown on the upper left of the graph. The presence of a shunt decreases
arterial PO2
for a given FIO2
.
As
T).
Assumptions are shown on the upper left of the graph. The presence of a shunt decreases
arterial PO2
for a given FIO2
.
As ![]() S/
S/![]() T
increases, supplemental O2
has progressively less effect on arterial PO2
.
(Adapted from Benumof JL: Anesthesia for Thoracic Surgery, 2nd ed. Philadelphia,
WB Saunders, 1995, and Lawler PGP, Nunn JF: A reassessment of the validity of the
iso-shunt graph. Br J Anaesth 56:1325, 1984.)
T
increases, supplemental O2
has progressively less effect on arterial PO2
.
(Adapted from Benumof JL: Anesthesia for Thoracic Surgery, 2nd ed. Philadelphia,
WB Saunders, 1995, and Lawler PGP, Nunn JF: A reassessment of the validity of the
iso-shunt graph. Br J Anaesth 56:1325, 1984.)
Right-to-left shunting is a special case of V̇A/![]() mismatch, with a V̇A/
mismatch, with a V̇A/![]() ratio of zero. Blood
flowing through a right-to-left shunt, whether intrapulmonary or intracardiac, has
gas tensions equal to mixed venous values. The net effect on arterial PO2
and PCO2
depends on the magnitude of the
shunt ( Fig. 36-3
) and the
mixed venous and pulmonary capillary gas tensions. Because major determinant of
mixed venous PO2
(and to a lesser extent
mixed venous PCO2
) is cardiac output (
ratio of zero. Blood
flowing through a right-to-left shunt, whether intrapulmonary or intracardiac, has
gas tensions equal to mixed venous values. The net effect on arterial PO2
and PCO2
depends on the magnitude of the
shunt ( Fig. 36-3
) and the
mixed venous and pulmonary capillary gas tensions. Because major determinant of
mixed venous PO2
(and to a lesser extent
mixed venous PCO2
) is cardiac output (![]() ),
changes in
),
changes in ![]() may modify the degree to which arterial PO2
is determined by pulmonary gas exchange ( Fig.
36-4
).
may modify the degree to which arterial PO2
is determined by pulmonary gas exchange ( Fig.
36-4
).
Diffusion nonequilibrium can exist when the gas tensions in the pulmonary capillary erythrocyte (Pc'O2 , Pc'CO2 ) are not equal to the alveolar gas tensions. This can occur under two physiologic conditions: increased pulmonary blood flow such that the erythrocyte does not have sufficient time in the alveoli to enable gas tensions to reach equilibrium or a thickening of the alveolar-capillary membrane such that the rate of diffusion of gas from alveolus to capillary (O2 ) or vice versa (CO2 ) is slowed. For CO2 diffusion, nonequilibrium would result in an arterial PCO2 (PaCO2 ) value higher than that of PACO2 . For O2 , nonequilibrium means that PaO2 is less than PAO2 . In practice, there has never been any evidence for failure of diffusion equilibrium of CO2 . Despite much discussion of O2 diffusion nonequilibrium, it probably rarely exists in clinical medicine. There is evidence for its existence during moderate exercise in patients with interstitial fibrosis and during severe exercise in normal individuals, particularly at higher altitudes.[7] In anesthesia or critical care, O2 diffusion nonequilibrium would probably occur only under very unusual circumstances, such as a septic patient with high cardiac output breathing air at the top of Pike's Peak (i.e., altitude of 4301m and barometric pressure of 444 mm Hg).
The following are the most likely causes of low PaO2 :
A common measurement used to assess the adequacy of pulmonary
gas exchange is the alveolar-arterial (A-a) gradient:
A-a gradient = PAO2
− PaO2
(7)
Calculation of the A-a gradient takes into account
any degree of hypoventilation or low inspired PO2
such that an abnormally high A-a gradient reflects
a V̇A/![]() mismatch (more specifically, low
V̇A/
mismatch (more specifically, low
V̇A/![]() in gas exchange units) or shunt.
The normal value of A-a gradient for a child or young
adult is less than 10 mm Hg, with an increase due to aging[14]
according to the following formula:
in gas exchange units) or shunt.
The normal value of A-a gradient for a child or young
adult is less than 10 mm Hg, with an increase due to aging[14]
according to the following formula:
A-a gradient = 0.21 ×
(age in years + 2.5) (8)
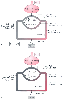 Figure 36-4
Effect of cardiac output on PO2
.
A, Arterial and mixed venous O2
tension
and content are shown at a cardiac output of 5 L/min. B,
Assuming a constant V̇O2
, an increase
in cardiac output to 8 L/min increases the PaO2
from 78 to 85 mm Hg. This occurs because Sv̄O2
increases at higher cardiac output. The resulting increase in O2
content
of the shunted blood (here assumed to be 10% of cardiac output) then raises arterial
O2
content and PaO2
. PO2
values are in mm Hg, and O2
content is in mL/dL.
Figure 36-4
Effect of cardiac output on PO2
.
A, Arterial and mixed venous O2
tension
and content are shown at a cardiac output of 5 L/min. B,
Assuming a constant V̇O2
, an increase
in cardiac output to 8 L/min increases the PaO2
from 78 to 85 mm Hg. This occurs because Sv̄O2
increases at higher cardiac output. The resulting increase in O2
content
of the shunted blood (here assumed to be 10% of cardiac output) then raises arterial
O2
content and PaO2
. PO2
values are in mm Hg, and O2
content is in mL/dL.
There is considerable scatter of the data around the mean values predicted by the relationship in Equation 8, with individual values for the A-a gradient exceeding 30 mm Hg. The A-a gradient also increases with abnormalities of pulmonary gas exchange. The usefulness of the A-a gradient may be demonstrated by an example. Interpretation of the following arterial blood gases in an unconscious individual in an emergency room (breathing room air) may be aided by calculating the A-a gradient: PaO2 = 50 mm Hg, PaCO2 = 76 mm Hg, and pH = 7.17. Assuming that barometric pressure = 760 mm Hg, body temperature = 37°C (therefore PH2 O = 47 mm Hg), and R = 0.8 (in this case using Equation 2), PAO2 = 59 mm Hg. The A-a gradient therefore equals 59 − 50 = 9 mm Hg, a normal value. Because the impairment of arterial oxygenation is associated with a normal A-a gradient, there is no intrinsic abnormality of pulmonary gas exchange. The diagnosis is most likely central respiratory depression.
A problem with the clinical use of the A-a gradient is that its normal value is highly dependent on inspired O2 concentration. As FIO2 increases, the A-a gradient becomes larger. In a normal individual breathing 100% O2 , the A-a gradient can exceed 70 mm Hg. A more useful parameter that obviates this problem is the a/A ratio (i.e., PaO2 /PAO2 ). Empirically, the a/A ratio has been shown to be relatively constant with varying FIO2 , [15] even in a hyperbaric chamber up to an ambient pressure of 3 atm absolute (see Chapter 70 ). The normal a/A ratio is 0.85; lower values indicate impaired pulmonary gas exchange.
If mixed venous blood is available for analysis, a solution can be found for a simplified but clinically useful compartmental model of the lung. This three-compartment model assumes the following division of gas exchange units within the lung:
Shunt fraction (venous admixture)
is the proportion of total blood flow perfusing the shunt compartment and can be
calculated from the following equation:
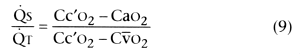
In Equation 9, ![]() S is shunt blood flow, and
S is shunt blood flow, and ![]() T
is cardiac output. Cc'o2
, Cao2
, and Cv̄o2
are the O2
contents of end-capillary, arterial, and mixed venous blood,
respectively. Cao2
and Cv̄o2
can be calculated directly.
Cc'o2
must be calculated from PAo2
and the Hb-O2
dissociation curve.
T
is cardiac output. Cc'o2
, Cao2
, and Cv̄o2
are the O2
contents of end-capillary, arterial, and mixed venous blood,
respectively. Cao2
and Cv̄o2
can be calculated directly.
Cc'o2
must be calculated from PAo2
and the Hb-O2
dissociation curve.
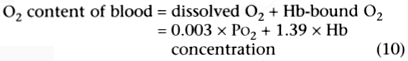
In Equation 10, the O2
content is given in mL/dL; PO2
is in mm Hg; and the hemoglobin concentration is in g/dL.
If PAO2
is high enough
that end-capillary blood has a hemoglobin O2
saturation close to 100%,
by dividing numerator and denominator by the O2
capacity (i.e. O2
content at 100% saturation) Equation 8 can be rewritten as the following approximation:

![]() S/
S/![]() T calculated
using either equation (i.e., using O2
as the "marker gas") includes gas
exchange units of low V̇A/
T calculated
using either equation (i.e., using O2
as the "marker gas") includes gas
exchange units of low V̇A/![]() in addition
to pure shunt. Breathing 100% O2
, however, eliminates the contribution
of low V̇A/
in addition
to pure shunt. Breathing 100% O2
, however, eliminates the contribution
of low V̇A/![]() gas exchange units to
gas exchange units to ![]() S/
S/![]() T
because any lung unit with nonzero V̇A/
T
because any lung unit with nonzero V̇A/![]() fully saturates with O2
the capillary blood perfusing it. Use of this
technique to assess shunt is complicated by the fact that breathing 100% O2
results in the progressive development of resorption atelectasis and a parallel increase
in shunt.[16]
fully saturates with O2
the capillary blood perfusing it. Use of this
technique to assess shunt is complicated by the fact that breathing 100% O2
results in the progressive development of resorption atelectasis and a parallel increase
in shunt.[16]
Whereas pathology that affects pulmonary O2
exchange
(typically low V̇A/![]() or shunt) can be detected
by inspection of the arterial blood gases and FIO2
(or formal calculation of the a/A ratio), lung abnormalities
that affect pulmonary CO2
exchange (typically high V̇A/
or shunt) can be detected
by inspection of the arterial blood gases and FIO2
(or formal calculation of the a/A ratio), lung abnormalities
that affect pulmonary CO2
exchange (typically high V̇A/![]() gas exchange units or dead space) require additional information. To measure physiologic
dead space (VDS), the Bohr equation can be used:
gas exchange units or dead space) require additional information. To measure physiologic
dead space (VDS), the Bohr equation can be used:
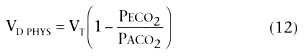
In Equation 12, PECO2
is the mixed expired
PCO2
and VT
is the tidal volume. PACO2
can be assumed
equal to PaCO2
(i.e., Enghoff modification).
To measure PECO2
, expired gas must be
analyzed in a mixing box, or a bag must be used to collect several expired breaths.
Alternatively, PECO2
can be measured
by placing a CO2
sensor in a bypass flow-mixing chamber (i.e., bymixer)
in the expiration limb of an anesthesia or ventilator circuit ( Fig.
36-5
).[17]
The dead space calculated
using this equation includes anatomic and physiologic dead space, as well as external
dead space such as in the breathing circuit. Dead space can also be measured on
a breath-by-breath basis if a volume capnogram is used (see Fig.
36-17
). Dead space measured using this formula (i.e., total physiologic
dead space) includes airway dead space (i.e., anatomic or series dead space) and
alveolar dead space (i.e., intrapulmonary or parallel dead space). Dead space is
usually expressed as a fraction of the tidal volume (VD/VT
ratio).
Mixed expired gas analysis is often not clinically available,
but an assessment of dead space ventilation may be made by examining the relationship
between minute ventilation (V̇E) and PaCO2
.
V̇E is continuously displayed by modern ventilators,
including anesthesia ventilators, and can be measured in spontaneously breathing
individuals by using a spirometer. Assuming normal V̇CO2
,
the following equation[18]
describes an empirical
relationship:
V̇E × PaCO2
≤ 8 W (13)
In Equation 13, W is the body weight. If V̇E
(L/min) times PaCO2
(mm Hg) exceeds eight
times the body weight (kg), an increase in dead space exists, indicating that to
maintain a normal PaCO2
, higher than usual
ventilation is required. V̇E ×
PaCO2
can also be elevated
by increased CO2
production (e.g., shivering, fever, metabolic acidosis).
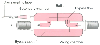 Figure 36-5
Bymixer. This compartment, placed in the expiratory
limb of a circle system, provides a mixing chamber through which a portion of the
exhaled gas flows. Mixing of gas within this chamber provides constant mixed expired
O2
and CO2
concentrations, from which V̇O2
,
V̇CO2
, and dead space can be calculated.
(Adapted from Breen PH, Serina ER: Bymixer provides on-line calibration
of measurement of CO2
volume exhaled per breath. Ann Biomed Eng 25:164,
1997.)
Figure 36-5
Bymixer. This compartment, placed in the expiratory
limb of a circle system, provides a mixing chamber through which a portion of the
exhaled gas flows. Mixing of gas within this chamber provides constant mixed expired
O2
and CO2
concentrations, from which V̇O2
,
V̇CO2
, and dead space can be calculated.
(Adapted from Breen PH, Serina ER: Bymixer provides on-line calibration
of measurement of CO2
volume exhaled per breath. Ann Biomed Eng 25:164,
1997.)
Using the respiratory gases to assess pulmonary gas exchange has
some drawbacks. First, the relationship between partial pressure and gas content
is nonlinear for both O2
and CO2
. Alterations in cardiac output,
hemoglobin concentration (resulting in altered venous blood gas tensions), or inspired
gas composition may lead to different calculated values of ![]() S/
S/![]() T
or VD/VT even if
actual V̇A/
T
or VD/VT even if
actual V̇A/![]() ratios in the lung are unchanged.
[19]
Second, changes in O2
or CO2
exchange can provide information only on a limited portion of the spectrum of V̇A/
ratios in the lung are unchanged.
[19]
Second, changes in O2
or CO2
exchange can provide information only on a limited portion of the spectrum of V̇A/![]() ratios. An increase in calculated
ratios. An increase in calculated ![]() S/
S/![]() T
(Equation 9) cannot distinguish between a shift to lower V̇A/
T
(Equation 9) cannot distinguish between a shift to lower V̇A/![]() ratios and an increase in true shunt.
ratios and an increase in true shunt.
In a more sophisticated technique described by Wagner and coworkers,
[16]
[20]
a dilute
mixture of several inert (i.e., not metabolically active) tracer gases is infused
intravenously. The ratio of partial pressures Pc'/Pv̄ or PA/Pv̄
at a gas exchange unit is described by the following equation:
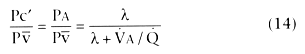
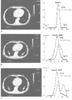 Figure 36-6
Effect of anesthesia on pulmonary atelectasis and gas
exchange. A, Computed tomography of the chest of
an awake patient. Adjacent to the scan is the distribution of ventilation (open
circles) and perfusion (solid circles)
in a 50-compartment lung model, determined by using the multiple inert gas method.
A unimodal distribution is shown for the awake individual with a shunt fraction
(
Figure 36-6
Effect of anesthesia on pulmonary atelectasis and gas
exchange. A, Computed tomography of the chest of
an awake patient. Adjacent to the scan is the distribution of ventilation (open
circles) and perfusion (solid circles)
in a 50-compartment lung model, determined by using the multiple inert gas method.
A unimodal distribution is shown for the awake individual with a shunt fraction
(![]() S/
S/![]() T)
of 0.8%. B, After a period of general anesthesia
with positive-pressure ventilation, crescent-shaped areas of increased tissue density
(arrows) appear in posterior lung regions. Corresponding
to these changes are a widening of both V̇A and
T)
of 0.8%. B, After a period of general anesthesia
with positive-pressure ventilation, crescent-shaped areas of increased tissue density
(arrows) appear in posterior lung regions. Corresponding
to these changes are a widening of both V̇A and
![]() distributions and an increase in
distributions and an increase in ![]() S/
S/![]() T
to 7.4%. C, The scan and data are shown for the same
individual after application of 10 cm H2
O of PEEP. Very little change
is observed in the areas of atelectasis, and V̇A/
T
to 7.4%. C, The scan and data are shown for the same
individual after application of 10 cm H2
O of PEEP. Very little change
is observed in the areas of atelectasis, and V̇A/![]() matching is further worsened, with the development of a bimodal ventilation distribution
and a further increase in
matching is further worsened, with the development of a bimodal ventilation distribution
and a further increase in ![]() S/
S/![]() T
to 11.1%. These changes are accompanied by a drop in PaO2
from 162 to 137 mm Hg. (Adapted from Tokics L, Hedenstierna G, Strandberg
A, et al: Lung collapse and gas exchange during general anesthesia: Effects of
spontaneous breathing, muscle paralysis and positive end-expiratory pressure. Anesthesiology
66:157, 1987.)
T
to 11.1%. These changes are accompanied by a drop in PaO2
from 162 to 137 mm Hg. (Adapted from Tokics L, Hedenstierna G, Strandberg
A, et al: Lung collapse and gas exchange during general anesthesia: Effects of
spontaneous breathing, muscle paralysis and positive end-expiratory pressure. Anesthesiology
66:157, 1987.)
In this technique of multiple inert gas (MIG) elimination, the
six gases typically used are sulfur hexafluoride, ethane, cyclopropane, enflurane,
diethyl ether, and acetone, spanning a partition coefficient of about 70,000. Each
gas provides information about a particular region in the spectrum of V̇A/![]() ,
permitting a multiple-compartment model to be calculated. The MIG method has been
used to demonstrate the development of V̇A/
,
permitting a multiple-compartment model to be calculated. The MIG method has been
used to demonstrate the development of V̇A/![]() mismatching and shunt during general anesthesia.[21]
Figure 36-6
demonstrates
the use of MIG to calculate a 50-compartment model of V̇A/
mismatching and shunt during general anesthesia.[21]
Figure 36-6
demonstrates
the use of MIG to calculate a 50-compartment model of V̇A/![]() .
Using this model, shunt fraction assessed by using the MIG method has been correlated
with atelectatic areas in dependent lung regions visible on chest computed tomography
(CT) (see Fig. 36-5
).[22]
[23]
The MIG method has been used to demonstrate
improved V̇A/
.
Using this model, shunt fraction assessed by using the MIG method has been correlated
with atelectatic areas in dependent lung regions visible on chest computed tomography
(CT) (see Fig. 36-5
).[22]
[23]
The MIG method has been used to demonstrate
improved V̇A/![]() matching
matching
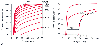 Figure 36-7
Hemoglobin-oxygen (OXYHb) saturation versus inspired
partial pressure of oxygen (PO2
). The
curves are plotted by changing inspired PO2
in a stepwise fashion. A, A series of theoretical
curves obtained by calculating the effect of different degrees of right-to-left shunt.
Increasing shunt displaces the curves downward. B,
The curve on the left of the graph (0%) is from a normal subject. The middle curve
(30%) represented a 30% right-to-left shunt from the 30% curve seen in A.
The curve on the right of this graph is from a patient undergoing thoracotomy for
esophageal surgery. The points cannot be fitted by any of the shunt curve, but the
fit is quite good when the 30% curve is shifted to the right. This implies a combination
of shunt and V̇A/
Figure 36-7
Hemoglobin-oxygen (OXYHb) saturation versus inspired
partial pressure of oxygen (PO2
). The
curves are plotted by changing inspired PO2
in a stepwise fashion. A, A series of theoretical
curves obtained by calculating the effect of different degrees of right-to-left shunt.
Increasing shunt displaces the curves downward. B,
The curve on the left of the graph (0%) is from a normal subject. The middle curve
(30%) represented a 30% right-to-left shunt from the 30% curve seen in A.
The curve on the right of this graph is from a patient undergoing thoracotomy for
esophageal surgery. The points cannot be fitted by any of the shunt curve, but the
fit is quite good when the 30% curve is shifted to the right. This implies a combination
of shunt and V̇A/![]() mismatch. (Adapted
from Jones JG, Jones SE: Discriminating between the effect of shunt and reduced
VA/Q on arterial oxygen saturation is particularly
useful in clinical practice. J Clin Monit Comput 16:337, 2000.)
mismatch. (Adapted
from Jones JG, Jones SE: Discriminating between the effect of shunt and reduced
VA/Q on arterial oxygen saturation is particularly
useful in clinical practice. J Clin Monit Comput 16:337, 2000.)
A noninvasive method of assessing the independent effects of shunt
and V̇A/![]() mismatching on arterial PO2
is to plot simultaneously arterial O2
saturation versus inspired PO2
( Fig. 36-7
).[30]
mismatching on arterial PO2
is to plot simultaneously arterial O2
saturation versus inspired PO2
( Fig. 36-7
).[30]
|
|
|
|
|
|
|
|
|
|
|
|
|