Oxygen and Carbon Dioxide Transport

Alveolar and Dead Space Ventilation and Alveolar Gas Tensions

In normal lungs, approximately two thirds of each breath reaches perfused alveoli to take part in gas exchange. This constitutes the effective or alveolar ventilation (V̇A). The remaining third of each breath takes no part in gas exchange and is therefore termed the total (or physiologic) dead space ventilation (VD). The relationship is as follows: alveolar ventilation (V̇A) = frequency (f) (VT − VD). The physiologic (or total) dead space ventilation (VD_physiologic ) may be further divided into two components: a volume of gas that ventilates the conducting airways, the anatomic dead space (VD_anatomic ), and a volume of gas that ventilates unperfused alveoli, the alveolar dead space (VD_alveolar ). Clinical examples of VD_alveolar ventilation include zone 1, pulmonary embolus, and destroyed alveolar septa, and such ventilation therefore does not participate in gas exchange. Figure 17-21 shows a two-compartment model of the lung in which the anatomic and alveolar dead space compartments have been combined into the total (physiologic) dead space compartment; the other compartment is the alveolar ventilation compartment, whose idealized V̇A/ ratio is 1.0.

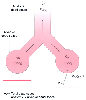Figure 17-21 Two-compartment model of the lung in which the anatomic and alveolar dead space compartments have been combined into the total (physiologic) dead space (VD). FACO₂ = alveolar CO₂ fraction; FECO₂ = mixed expired CO₂ fraction; FICO₂ = inspired CO₂ fraction; V̇A = alveolar ventilation; V̇A/ = 1 means ventilation and perfusion are equal in liters per minute; V̇CO₂ = carbon dioxide production; V̇E = expired minute ventilation. Normally, the amount of CO₂ eliminated at the airway (V̇E × FECO₂ ) equals the amount of CO₂ removed by alveolar ventilation (V̇A × FACO₂ ) because there is no CO₂ elimination from alveolar dead space (FICO₂ = 0).

The anatomic dead space varies with lung size and is approximately 2 mL/kg of body weight (150 mL in a 70-kg adult). In a normal healthy adult lying supine, anatomic dead space and total (physiologic) dead space are approximately equal to each other because alveolar dead space is normally minimal. In the erect posture, the uppermost alveoli may not be perfused (zone 1), and alveolar dead space may increase from a negligible amount to 60 to 80 mL.

Figure 17-21 illustrates that in a steady state, the volume of CO₂ entering the alveoli (V̇CO₂ ) is equal to the volume of CO₂ eliminated in the expired gas (V̇E)(FECO₂ ). Thus V̇CO₂ = (V̇E)(FECO₂ ). However, the expired gas volume consists of alveolar gas (V̇A)(FACO₂ ) and V̇D gas (V̇D)(FICO₂ ). Thus, V̇CO₂ = (V̇A)(FACO₂ ) + (V̇D)(FICO₂ ). Setting the first equation equal to the second equation and using the relationship V̇E = V̇A + V̇D, subsequent algebraic manipulation, including setting PACO₂ equal to PaCO₂ , results in the modified Bohr equation:

VD/VT = (PaCO₂ − PECO₂ )/PaCO₂ (9)

The PECO₂ value may be obtained by measuring exhaled CO₂ in a large (Douglas) bag, or more commonly, end-tidal PCO₂ (PETCO₂ ) can be used as a surrogate. In severe lung disease, physiologic VD/VT provides a useful expression of

698

The alveolar concentration of a gas is equal to the difference between the inspired concentration of a gas and the ratio of the output (or uptake) of the gas to V̇A. Thus, for gas X during dry conditions, PAX = (Pdry atm) (FIX) ± V̇X (output or uptake)/V̇A, where PAX = alveolar partial pressure of gas X, FIX = inspired concentration of gas X, Pdry atm = dry atmospheric pressure = Pwet atm − PH₂ O = 760 − 47 = 713 mm Hg, V̇X = output or uptake of gas X, and V̇A = alveolar ventilation.

For CO₂ , PACO₂ = 713(FICO₂ + V̇CO₂ /V̇A). Because FICO₂ = 0 and using standard conversion factors:

PACO₂ = 713[V̇CO₂ (mL/min STPD)/V̇A (L/min/BTPS)(0.863)] (10)

Figure 17-22 Relationship between minute ventilation (V̇E, L/min) and PaCO₂ for a family of ratios of total dead space to tidal volume (VD/VT). These curves are hyperbolic (see Equation 10) and rise steeply at low VE values.

For O₂ ,

PAO₂ = 713[FIO₂ − V̇O₂ (mL/min)/V̇A (mL/min)] (11)

For example, 100 mm Hg = 713(0.21 − 225/3200).

Figure 17-23 shows the hyperbolic relationships expressed in Equations 10 and 11 between PaCO₂ and V̇A (see Fig. 17-22 ) and between PAO₂ and V̇A for different levels of V̇CO₂ and V̇O₂ , respectively. PaCO₂ is substituted for PACO₂ because PACO₂ -to-PaCO₂ gradients are small (as opposed to PAO₂ -to-PaO₂ gradients, which can be large). Note that as V̇A increases, the second term of the right side of Equations 10 and 11 approaches zero and the composition of the alveolar gas approaches that of the inspired gas. In addition, it should be noted from Figure 17-22 , Figure 17-23 , and Figure 17-24 that because anesthesia is usually administered with an oxygen-enriched gas mixture, hypercapnia is a more common result of hypoventilation than hypoxemia is.

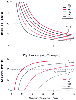Figure 17-23 The relationship between alveolar ventilation and PAO₂ and PaO₂ for a group of different O₂ consumption (V̇O₂ ) and CO₂ production (V̇CO₂ ) values is derived from Equations 10 and 11 in the text and is hyperbolic. As alveolar ventilation increases, PAO₂ and PaCO₂ approach inspired concentrations. Decreases in alveolar ventilation to less than 4 L/min are accompanied by precipitous decreases in PAO₂ and increases in PaCO₂ .

699

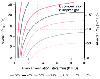Figure 17-24 For any given O₂ concentration in inspired gas, the relationship between alveolar ventilation and PAO₂ is hyperbolic. As the inspired O₂ concentration is increased, the amount that alveolar ventilation must decrease to produce hypoxemia is greatly increased. BTPS, body temperature, ambient pressure, saturated. (Redrawn from Lumb AB: Respiratory system resistance: Measurement of closing capacity. In Lumb AB [ed]: Nunn's Applied Respiratory Physiology, 5th ed. London, Butterworths, 2000, p 79.)

Oxygen Transport

Overview of Oxygen Transport

The principal function of the heart and lungs is supporting O₂ delivery to and CO₂ removal from the tissues in accordance with metabolic requirements while maintaining arterial blood O₂ and CO₂ partial pressures within a narrow range. The respiratory and cardiovascular systems are series-linked to accomplish this function over a wide range of metabolic requirements, which may increase 30-fold from rest to heavy exercise. The functional links in the oxygen transport chain are as follows: (1) ventilation and distribution of ventilation with respect to perfusion, (2) diffusion of O₂ into blood,

TABLE 17-3 -- Functional capacities and potential maximum O₂ transport of each link in the O₂ transport chain in normal humans * at sea level

Link in Chain	Functional Capacity in Normal Humans	Theoretical Maximum O2 Transport Capacity
Ventilation	200 L/min (MVV)	0.030 × MVV = 6.0 L O2 /min
Diffusion and chemical reaction		DLO2 = 6.1 L O2 /min
CO	20 L/min
O2 extraction	75%	0.16 × CO = 3.2 L O2 /min
(a-v O2 difference)	(16 mL O2 /100 mL or 0.16)
CO = cardiac output; MVV = maximum voluntary ventilation.
From Cassidy SS: Heart-lung interactions in health and disease. Am J Med Sci 30:451–461, 1987.

*Hemoglobin = 15 g/dL; physiologic dead space in percentage of tidal volume = 0.25; partial alveolar pressure of oxygen > 110 mm Hg.

(3) chemical reaction of O₂ with Hb, (4) T of arterial blood, and (5) distribution of blood to tissues and release of O₂ (

The maximum functional capacity of each link can be determined independently. Table 17-3 lists these measured functional capacities for healthy, young men. Because theoretical maximal O₂ transport at the ventilatory step or the diffusion and chemical reaction steps (about 6 L/min in healthy humans at sea level) exceeds the O₂ transportable by the maximum cardiac output and distribution steps, the limit to O₂ transport is the cardiovascular system. Respiratory diseases would not be expected to limit maximum O₂ transport until functional capacities are reduced nearly 40% to 50%.

Oxygen-Hemoglobin Dissociation Curve

As a red blood cell (RBC) passes by the alveolus, O₂ diffuses into plasma and increases PaO₂ . As PaO₂ increases, O₂ diffuses into the RBC and combines with Hb. Each Hb molecule consists of four heme molecules attached to a globin molecule. Each heme molecule consists of glycine, α-ketoglutaric acid, and iron in the ferrous (Fe²⁺ ) form. Each ferrous ion has the capacity to bind with one O₂ molecule in a loose, reversible combination. As the ferrous ions bind to O₂ , the Hb molecule begins to become saturated.

The oxy-Hb dissociation curve relates the saturation of Hb (rightmost y axis in Fig. 17-25 ) to PaO₂ . Hb is fully saturated (100%) by a PO₂ of about 700 mm Hg. The normal arterial point on the right side and flat part of the oxy-Hb curve in Figure 17-25 is 95% to 98% saturated by a PaO₂ of about 90 to 100 mm Hg. When PO₂ is less than 60 mm Hg (90% saturation), saturation falls steeply, and the amount of Hb uncombined with O₂ increases greatly for a given decrease in PO₂ . Mixed venous blood has a PO₂ (Pv̄O₂ ) of about 40 mm Hg and is approximately 75% saturated, as indicated by the middle of the three points on the oxy-Hb curve in Figure 17-25 .

700

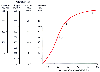Figure 17-25 Oxygen-hemoglobin dissociation curve. Four different ordinates are shown as a function of oxygen partial pressure (the abscissa). In order from right to left, they are saturation (%); O₂ content (mL of O₂ /0.1 L of blood); O₂ supply to peripheral tissues (mL/min); and O₂ available to peripheral tissues (mL/min), which is O₂ supply minus the approximately 200 mL/min that cannot be extracted below a partial pressure of 20 mm Hg. Three points are shown on the curve: a, normal arterial pressure; , normal mixed venous pressure; and P₅₀ , the partial pressure (27 mm Hg) at which hemoglobin is 50% saturated.

The oxy-Hb curve can also relate the O₂ content (CO₂ ) (vol%, mL of O₂ /0.1 L of blood; second most right y axis in Fig. 17-25 ) to PO₂ . Oxygen is carried in solution in plasma, 0.003 mL of O₂ /mm Hg PO₂ /0.1 L, and is combined with Hb, 1.39 mL of O₂ /g of Hb, to the extent (percentage) that Hb is saturated. Thus,

CO₂ = (1.39)(Hb)(percent saturation) + 0.003(PO₂ ) (12)

For a patient with an Hb content of 15 g/0.1 L, PaO₂ of 100 mm Hg, and Pv̄O₂ of 40 mm Hg, the arterial O₂ content (CaO₂ ) = (1.39)(15)(1) + (0.003)(100) = 20.9 + 0.3 = 21.2 mL of O₂ /0.1 L; the mixed venous O₂ content (Cv̄O₂ ) = (1.39) (15)(0.75) + (0.003)(40) = 15.6 + 0.1 = 15.7 mL of O₂ /0.1 L. Thus, the normal arteriovenous O₂ content difference is approximately 5.5 mL/0.1 L.

Note that Equation 12 uses the constant 1.39, which means that 1 g of Hb can carry 1.39 mL of oxygen. Controversy exists over the magnitude of this number. Originally, 1.34 had been used,^[95] but with determination of the molecular weight of Hb (64,458), the theoretical value of 1.39 became popular.^[96] After extensive human studies, Gregory^[97] observed in 1974 that the applicable value was 1.31 mL O₂ /g of Hb in human adults. The reason that the clinically measured CO₂ is lower than the theoretical 1.39 is probably due to the small amount of methemoglobin (Met-Hb) and carboxyhemoglobin (CO-Hb) normally present in blood.

The oxy-Hb curve can also relate O₂ transport (L/min) to the peripheral tissues (see the third most right y axis in Fig. 17-25 ) to PO₂ . This value is obtained by multiplying the O₂ content by T (O₂ transport = T ×CaO₂ ). To do this multiplication, one must convert the content unit of mL/0.1 L to mL/L by multiplying the usual O₂ content by 10 (results in mL of O₂ /L of blood); subsequent multiplication of mL/L against T in L/min yields mL/min. Thus, if T = 5 L/min and CaO₂ = 20 mL of O₂ /0.1 L, the arterial point corresponds to 1000 mL O₂ /min going to the periphery, and the venous point corresponds to 750 mL O₂ /min returning to the lungs, with V̇O₂ = 250 mL/min.

The oxy-Hb curve can also relate the O₂ actually available to the tissues (see leftmost y axis in Fig. 17-25 ) as a function of PO₂ . Of the 1000 mL/min of O₂ normally going to the periphery, 200 mL/min of O₂ cannot be extracted because it would lower PO₂ below the level (see the rectangular dashed line in Fig. 17-25 ) at which organs such as the brain can survive; the O₂ available to tissues is therefore 800 mL/min. This amount is approximately three to four times the normal resting V̇O₂ . When T = 5 L/min and arterial saturation is less than 40%, the total flow of O₂ to the periphery is reduced to 400 mL/min; the available O₂ is now 200 mL/min and O₂ supply just equals O₂ demand. Consequently, with low arterial saturation, tissue demand can be met only by an increase in T or, in the longer term, by an increase in Hb concentration.

The affinity of Hb for O₂ is best described by the PO₂ level at which Hb is 50% saturated (P₅₀ ) on the oxy-Hb curve. The normal adult P₅₀ is 26.7 mm Hg (see the point on the left side and steep portion of the oxy-Hb curve in Fig. 17-24 ).

The effect of a change in PO₂ on Hb saturation is related to both P₅₀ and the portion of the oxy-Hb curve at which the change occurs.^[98] In the region of normal PaO₂ (75 to 100 mm Hg), the curve is relatively horizontal, so shifts of the curve have little effect on saturation. In the region of mixed venous PO₂ , where the curve is relatively steep, a shift of the curve leads to a much greater

701

A P₅₀ higher than 27 mm Hg describes a right-shifted oxy-Hb curve, which means that at any given PO₂ , Hb has a low affinity for O₂ and is less saturated than normal. This higher P₅₀ may allow a lower tissue perfusion than normal to produce the normal amount of O₂ unloading. Causes of a right-shifted oxy-Hb curve are acidosis (metabolic and respiratory—the Bohr effect), hyperthermia, abnormal Hb, increased RBC 2,3-DPG content, and inhaled anesthetics (see later).^[98]

Abnormalities in acid-base balance result in alteration of 2,3-DPG metabolism to shift the oxy-Hb curve to its normal position. This compensatory change in 2,3-DPG requires between 24 and 48 hours. Thus, with acute acid-base abnormalities, O₂ affinity and the position of the oxy-Hb curve change. However, with more prolonged acid-base changes, the reciprocal changes in 2,3-DPG levels shift the oxy-Hb curve and therefore O₂ affinity back toward normal.^[98]

Many inhaled anesthetics have been shown to shift the oxy-Hb dissociation curve to the right.^[99] Isoflurane shifts P₅₀ to the right by 2.6 ± 0.07 mm Hg at a vapor pressure of approximately 1 minimum alveolar concentration (MAC) (1.25%).^[100] On the other hand, high-dose fentanyl, morphine, and meperidine do not alter the position of the curve.

Effect of S/T on PaO₂

PAO₂ is directly related to FIO₂ in normal patients. PAO₂ and FIO₂ also correspond to PaO₂ when there is little to no right-to-left transpulmonary shunt (S/T). Figure 17-26 shows the relationship between FIO₂ and PaO₂ for a family of right-to-left transpulmonary shunts (S/T); the calculations assume a constant and normal T and PaCO₂ . With no S/T, a linear increase in FIO₂ results in a linear increase in PaO₂ (solid straight line). As the shunt is increased, the S/T lines relating FIO₂ to PaO₂ become progressively flatter.^[101] With a shunt of 50% of QT, an increase in FIO₂ results in almost no increase in PaO₂ . The solution to the problem of hypoxemia secondary to a large shunt is not increasing the FIO₂ , but rather causing a reduction in the shunt (fiberoptic bronchoscopy, PEEP, patient positioning, antibiotics, suctioning, diuretics).

Effect of T and V̇O₂ on CaO₂

In addition to an increased S/T, CaO₂ is decreased by decreased T (for a constant V̇O₂ ) and by increased V̇O₂ (for a constant T). In either case (decreased T or

Figure 17-26 Effect of changes in inspired oxygen concentration on PaO₂ for various right-to-left transpulmonary shunts. Cardiac output (T), hemoglobin (Hb), oxygen consumption (V̇O₂ ), and arteriovenous oxygen content differences [C(a - v)O₂ ] are assumed to be normal.

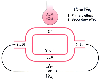Figure 17-27 Effect of a decrease in cardiac output or an increase in oxygen consumption on mixed venous and arterial oxygen content. Mixed venous blood () either perfuses ventilated alveolar (ALV O₂ ) capillaries and becomes oxygenated end-pulmonary capillary blood (c') or perfuses whatever true shunt pathways exist and remains the same in composition (desaturated). These two pathways must ultimately join together to form mixed arterial (a) blood. If cardiac output (T) decreases or oxygen consumption (V̇O₂ ) increases, or both the tissues must extract more oxygen per unit volume of blood than under normal conditions. Thus, the primary effect of a decrease in T or an increase in V̇O₂ is a decrease in mixed venous oxygen content. The mixed venous blood with a decreased oxygen content must flow through the shunt pathway as before (which may remain constant in size) and lower the arterial content of oxygen. Thus, the secondary effect of a decrease in T or an increase in V̇O₂ is a decrease in arterial oxygen content.

702

The amount of O₂ flowing through any given particular lung channel per minute, as depicted in Figure 17-27 , is a product of blood flow times the O₂ content of that blood. Thus, from Figure 17-27 , T × CaO₂ = c' × Cc'O₂ + S × Cv̄O₂ . With c' = T − S and further algebraic manipulation, ^[102]

S/T = Cc'O₂ − CaO₂ /Cc'O₂ − Cv̄O₂ (13)

The larger the intrapulmonary shunt, the greater is the decrease in CaO₂ because more venous blood with lower Cv̄O₂ can admix with end-pulmonary capillary blood (see Fig. 17-37 ). ^{[103] [104]} Thus, P(A - a)O₂ is a function both of the size of the S/T and of what is flowing through the S/T, namely, Cv̄O₂ , and Cv̄O₂ is a primary function of T and V̇O₂ .

Figure 17-28 shows the equivalent circuit of the pulmonary circulation in a patient with a 50% shunt, a normal Cv̄O₂ of 15 vol%, and a moderately low CaO₂ of 17.5 vol%. Decreasing T or increasing V̇O₂ , or both, causes a larger primary decrease in Cv̄O₂ to 10 vol% and a smaller, but still significant secondary decrease in CaO₂ to 15 vol%; the ratio of change in Cv̄O₂ to CaO₂ in this example of 50% S/T is 2:1.

Figure 17-28 The equivalent circuit of the pulmonary circulation in a patient with a 50% right-to-left shunt. Oxygen content is in mL/100 mL of blood (vol%). A decrease in cardiac output (T) or an increase in O₂ consumption (V̇O₂ ) can cause a decrease in mixed venous oxygen content (from 15 to 10 vol% in this example), which in turn will cause a decrease in the arterial content of oxygen (from 17.5 to 15.0 vol%). In this 50% shunt example, the decrease in mixed venous oxygen content was twice the decrease in arterial oxygen content.

If a decrease in T or an increase in V̇O₂ is accompanied by a decrease in S/T, there may be no change in PaO₂ (a decreasing effect on PaO₂ is offset by an increasing effect on PaO₂ ) ( Table 17-4 ). These changes sometimes occur in diffuse lung disease. If a decrease in T or an increase in V̇O₂ is accompanied by an increase in S/T, PaO₂ may be greatly decreased (a decreasing effect on PaO₂ is compounded by another decreasing effect on PaO₂ ) (see Table 17-4 ). These changes sometimes occur in regional ARDS and atelectasis. ^[105]

Fick Principle

The Fick principle allows calculation of V̇O₂ and states that the amount of O₂ consumed by the body (V̇O₂ ) is equal to the amount of O₂ leaving the lungs (T)(CaO₂ ) minus the amount of O₂ returning to the lungs (T)(CEO₂ ). Thus

V̇O₂ = (T)(CaO₂ ) − (T(Cv̄O₂ = T(CaO₂ − Cv̄O₂ )

Condensing the content symbols yields the usual expression of the Fick equation:

V̇O₂ = (T[C(a − v)O₂ ] (14)

This equation states that O₂ consumption is equal to T times the arteriovenous O₂ content difference. Normally, (5 L/min)(5.5 mL)/0.1 L = 0.27 L/min (see the section "Oxygen-Hemoglobin Dissociation Curve").

V̇O₂ = V̇E(FIO₂ ) − V̇E(FEO₂ ) = V̇E(FIO₂ − FEO₂ ) (15)

Similarly, the amount of O₂ consumed by the body (V̇O₂ ) is equal to the amount of O₂ brought into the lungs by ventilation (V̇I)(FIO₂ ) minus the amount of O₂ leaving the lungs by ventilation (V̇E)(FEO₂ ), where V̇E is expired minute ventilation and FEO₂ is the mixed expired O2 fraction.

Thus, V̇O₂ = (V̇I)(FIO₂ ) − (V̇E(FEO₂ ). Because the difference between V̇I and V̇E is due to the difference between V̇O₂ (normally 250 mL/min) and V̇CO₂ (normally 200 mL/min) and is only 50 mL/min (see later), V̇I essentially equals V̇E.

Normally, V̇O₂ = 5.0 L/min (0.21 − 0.16) = 0.25 L/min. In determining V̇O₂ in this way, V̇E can be measured with a spirometer, FIO₂ can be measured with an O₂ analyzer or from known fresh gas flows, and FEO₂ can be measured by collecting expired gas in a bag for a few minutes.

TABLE 17-4 -- Cardiac output (T), shunt (S/T), and venous (Pv̄O₂ ) and arterial (PaO₂ ) oxygenation

Changes	Clinical Situation
If T ↓ → ↓ Pv̄O2 and S/T = K → PaO2 ↓	Decreased cardiac output, stable shunt
If T ↓ → ↓ Pv̄O2 and S/T ↓ → PaO2 = K	Application of PEEP in ARDS
If T ↓ → ↓ Pv̄O2 and S/T ↑ → PaO2 ↓↓	Shock combined with ARDS or atelectasis
ARDS, adult respiratory distress syndrome; K, constant; PEEP, positive end expiratory pressure; ↓, decrease; ↑, increase.

703

Additionally, the Fick equation is useful in understanding the impact of changes in T on PaO₂ and Pv̄O₂ . If O₂ remains constant (K) and T decreases (↓), the arteriovenous O₂ content difference has to increase (↑):

V̇O₂ = K = (↓)T × (↑)C(a − )O₂ .

The C(a - )O₂ difference increases because a decrease in T causes a much larger and primary decrease in Cv̄O₂ versus a smaller and secondary decrease in CaO₂ :

(↑)C(a − )O₂ = C(↓ a − ↓ ↓ )O₂ ^[103]

Thus, Cv̄O₂ (and Pv̄O₂ ) are much more sensitive indicators of T because they change more with changes in T than CaO₂ (or PaO₂ ) does (see Fig 17-27 and Fig. 17-37 ).

Carbon Dioxide Transport

The amount of CO₂ circulating in the body is a function of both CO₂ elimination and production. Elimination of CO₂ depends on pulmonary blood flow and alveolar ventilation. Production of CO₂ (V̇CO₂ ) parallels O₂ consumption (V̇O₂ ) according to the respiratory quotient (R):





Under normal resting conditions, R is 0.8; that is, only 80% as much CO₂ is produced as O₂ is consumed. However, this value changes as the nature of the metabolic substrate changes. If only carbohydrate is used, the respiratory quotient is 1.0. Conversely, with the sole use of fat, more O₂ combines with hydrogen to produce water, and the R value drops to 0.7.

CO₂ is transported from mitochondria to the alveoli in a number of forms. In plasma, CO₂ exists in physical solution, hydrated to carbonic acid (H₂ CO₃ ), and as bicarbonate (HCO₃ ^- ). In the RBC, CO₂ combines with Hb as carbaminohemoglobin (Hb-CO₂ ). The approximate relative values of H₂ CO₃ (H₂ O + CO₂ ), HCO₃ ^- , and Hb-CO₂ to the total CO₂ transported are 7%, 80%, and 13%, respectively.

In plasma, CO₂ exists both in physical solution and as H₂ CO₃ :

H₂ O + CO₂ H2CO₃ (17)

The CO₂ in solution can be related to PCO₂ by the use of Henry's law^[106] :

PCO₂ × α = [CO₂ ] in solution (18)

where α is the solubility coefficient of CO₂ in plasma (0.03 mmol/L/mm Hg at 37°C). However, the major fraction of CO₂ produced passes into the RBC. As in plasma, CO₂ combines with water to produce H₂ CO₃ . However, unlike the slow reaction in plasma, in which the equilibrium point lies toward the left, the reaction in an RBC is catalyzed by the enzyme carbonic anhydrase. This zinc-containing enzyme moves the reaction to the right at a rate 1000 times faster than in plasma. Furthermore, nearly 99.9% of the H₂ CO₃ dissociates to HCO₃ ^- and hydrogen ions (H⁺ ):





The H⁺ produced from H₂ CO₃ in the production of HCO₃ ^- is buffered by Hb (H⁺ + Hb HHb). The HCO₃ ^- produced passes out of the RBC into plasma to perform its function as a buffer. To maintain electrical neutrality within the RBC, chloride ion (Cl^- ) moves in as HCO₃ ^- moves out (Cl^- shift). Finally, CO₂ can combine with Hb in the erythrocyte (to produce Hb-CO₂ ). Again, as in HCO₃ ^- release, an H⁺ ion is formed in the reaction of CO₂ and Hb. This H⁺ ion is also buffered by Hb.

Bohr and Haldane Effects

Just as the percent saturation of Hb with O₂ is related to PO₂ (described by the oxy-Hb curve), so is the total CO₂ in blood related to PCO₂ . Additionally, Hb has variable affinity for CO₂ ; it binds more avidly in the reduced state than as oxy-Hb.^[98] The Bohr effect describes the effect of PCO₂ and [H⁺ ] ions on the oxy-Hb curve. Hypercapnia and acidosis both shift the curve to the right (reducing the oxygen-binding affinity of hemoglobin), and hypocapnia and alkalosis both shift the curve to the left. Conversely, the Haldane effect describes the shift in the CO₂ dissociation curve caused by oxygenation of Hb. Low PO₂ shifts the CO₂ dissociation curve to the left so that the blood is able to pick up more CO₂ , as occurs in capillaries of rapidly metabolizing tissues). Conversely, oxygenation of Hb (as occurs in the lungs) reduces the affinity of Hb for CO₂ , and the CO₂ dissociation curve is shifted to the right, thereby increasing CO₂ removal.