Other (Nongravitational) Important Determinants of Pulmonary Compliance, Resistance, Lung Volume, and Ventilation

Pulmonary Compliance

For air to flow into the lungs, a pressure gradient (ΔP) must be developed to overcome the elastic resistance of the lungs and chest wall to expansion. These structures are arranged concentrically, and their elastic resistance is therefore additive. The relationship between ΔP and the resultant volume increase (ΔV) of the lungs and thorax is independent of time and is known as total compliance (CT), as expressed in the following equation:

CT (L/cm H₂ O) = ΔV (L)/ΔP (cm H₂ O) (1)

The CT of lung plus chest wall is related to the individual compliance of the lungs (CL) and chest wall (CCW) according to the following expression:

1/CT = 1/CL + 1/CCW
[or CT = (CL)(CCW)/CL + CCW] (2)

Normally, CL and CCW each equal 0.2 L/cm H₂ O; thus, CT = 0.1 L/cm H₂ O. To determine CL, ΔV and the transpulmonary pressure gradient (PA - Ppl, the ΔP for the lung) must be known; to determine CCW, ΔV and the transmural pressure gradient (Ppl - Pambient, the ΔP for the chest wall) must be known; and to determine CT, ΔV and the transthoracic pressure gradient (PA - Pambient, the ΔP for the lung and chest wall together) must be known. In clinical practice, only CT is measured, which can be done dynamically or statically, depending on whether a peak or plateau inspiratory ΔP (respectively) is used for the CT calculation.

During a positive- or negative-pressure inspiration of sufficient duration, transthoracic ΔP first increases to a peak value and then decreases to a lower plateau value. The peak transthoracic pressure value is due to the pressure required to overcome both elastic and airway resistance (see the section "Airway Resistance"). Transthoracic pressure decreases to a plateau value after the peak value because with time, gas is redistributed from stiff alveoli (which expand only slightly and therefore have only a short inspiratory period) into more compliant alveoli (which expand a great deal and therefore have a long inspiratory period). Because the gas is redistributed into more compliant alveoli, less pressure is required to contain the same amount of gas, which explains why the pressure decreases. In practical terms, dynamic compliance is the volume change divided by the peak inspiratory transthoracic pressure, and static compliance is the volume change divided by the plateau inspiratory transthoracic pressure. Therefore, static CT is usually greater than dynamic CT because the former calculation uses a smaller denominator (lower pressure) than the latter. However, if the patient is receiving PEEP, this pressure must first be subtracted from the peak or plateau pressure before calculating thoracic compliance (i.e., compliance = volume delivered/peak or plateau pressure − PEEP).

PA deserves special comment. The alveoli are lined with a layer of liquid. The lining of a curved surface (sphere or cylinder, such as the alveoli, bronchioles, and bronchi) with liquid creates a surface tension that tends to make the surface area that is exposed to the atmosphere as small as possible. Simply stated, water molecules crowd much closer together on the surface of a curved layer of water than elsewhere in the fluid. As lung or

690

According to the Laplace expression (Equation 3), the pressure in an alveolus (P, in dynes per square centimeter) is higher than ambient pressure by an amount that depends on the surface tension of the lining liquid (T, in dynes per centimeter) and the radius of curvature of the alveolus (R, in centimeters). This relationship is expressed in the following equation:

P = 2T/R (3)

Although surface tension contributes to the elastic resistance and retractive forces of the lung, two difficulties must be resolved. First, the pressure inside small alveoli should be higher than that inside large alveoli, a conclusion that stems directly from the Laplace equation (R in the denominator). From this reasoning, one would expect a progressive discharge of each small alveolus into a larger one until eventually only one gigantic alveolus would be left ( Fig. 17-11A ). The second problem concerns the relationship between lung volume and transpulmonary ΔP (PA - Ppl). Theoretically, the retractive forces of the lung should increase as lung volume decreases. If this were true, lung volume should decrease in a vicious circle, with an increasingly progressive tendency to collapse as lung volume diminishes.

These two problems are resolved by the fact that the surface tension of the fluid lining the alveoli is variable and decreases as its surface area is reduced. The surface tension of alveolar fluid can reach levels that are well below the normal range for body fluids such as water and plasma. When an alveolus decreases in size, the surface

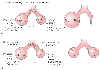Figure 17-11 Relationship between surface tension (T), alveolar radius (R), and alveolar transmural pressure (P). The left side of the diagrams shows the starting condition. The right side of the diagrams shows the expected result in alveolar size (using the Laplace equation to calculate the starting pressure). In the upper example (A), the surface tension in the fluid lining both the large and the small alveolus is the same (no surfactant). Accordingly, the direction of gas flow is from the higher-pressure small alveolus to the lower-pressure large alveolus, which results in one large alveolus (R_final = ΣR_initial ). In the bottom example (B), the expected changes in surface tension when surfactant lines the alveolus are shown (less tension in the smaller alveolus). The direction of gas flow is from the larg er alveolus to the smaller alveolus until the two alveoli are of equal size and are volume stable (R_K ). K, constant; ΣR, sum of all individual radii.

The substance responsible for the reduction (and variability) in alveolar surface tension is secreted by the intra-alveolar type II pneumocyte and is a lipoprotein called surfactant, which floats as a 50-Å-thick film on the surface of the fluid lining the alveoli. When the surface film is reduced in area and the concentration of surfactant at the surface is increased, the surface-reducing pressure is increased and counteracts the surface tension of the fluid lining the alveoli.

Airway Resistance

For air to flow into the lungs, ΔP (pressure gradient) must also be developed to overcome the nonelastic airway resistance of the lungs to airflow. The relationship between ΔP and the rate of airflow (V̇) is known as airway resistance (R):





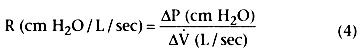
The ΔP along the airway depends on the caliber of the airway and the rate and pattern of airflow. There are three main patterns of airflow. Laminar flow occurs when the gas passes down parallel-sided tubes at less than a certain critical velocity. With laminar flow, the pressure drop down the tube is proportional to the flow rate

691

When flow exceeds the critical velocity, it becomes turbulent. The significant feature of turbulent flow is that the pressure drop along the airway is no longer directly proportional to the flow rate but is proportional to the square of the flow rate according to Equation 6 for turbulent flow:

ΔP = V̇² pfL/4π² r⁵ (6)

In Equation 6, p is the density of the gas (or liquid), and f is a friction factor that depends on the roughness of the tube wall.^[73] Thus, with increases in turbulent flow (and/or orifice flow; see the next paragraph), ΔP increases much more than V̇, and therefore airway resistance (R) increases more also, as predicted by Equation 4.

Orifice flow occurs at severe constrictions such as a nearly closed larynx or a kinked endotracheal tube. In these situations, the pressure drop is also proportional to the square of the flow rate, but density replaces viscosity as the important factor in the numerator. This explains why a low-density gas such as helium diminishes the resistance to flow (by threefold in comparison to air) in severe obstruction of the upper airway.

Because the total cross-sectional area of the airways increases as branching occurs, the velocity of airflow decreases distal in the airways; laminar flow is therefore chiefly confined to the airways below the main bronchi. Orifice flow occurs at the larynx, and flow in the trachea is turbulent during most of the respiratory cycle. By viewing the components that constitute each of the preceding airway pressure equations one can see that many factors may obviously affect the pressure drop down the airways during respiration. However, variations in diameter of the smaller bronchi and bronchioles are particularly critical (bronchoconstriction may convert laminar flow to turbulent flow), and the pressure drop along the airways may become much more closely related to the flow rate.

Different Regional Lung Time Constants

Thus far, the compliance and airway resistance properties of the chest have been discussed separately. In the following analysis, pressure at the mouth is assumed to increase suddenly to a fixed positive value^[74] ( Fig. 17-12 ) that overcomes both elastic and airway resistance and to be maintained at this value during inflation of the lungs. The ΔP required to overcome nonelastic airway resistance is the difference between the fixed mouth pressure and the instantaneous height of the dashed line in Figure 17-12 and is proportional to the flow rate during most of the respiratory cycle. Thus, the ΔP required to overcome nonelastic airway resistance is maximal initially but then decreases exponentially ( Fig. 17-12A, hatched lines ). The rate of filling therefore also declines in an approximately exponential manner. The remainder of the pressure gradient overcomes the elastic resistance (the instantaneous height of the dashed line in Fig. 17-12A ) and is proportional to the change in lung volume. Thus, the ΔP required to overcome elastic resistance is minimal initially but then increases exponentially, as does lung volume. Alveolar filling ceases (lung volume remains constant) when the pressure resulting from the retractive

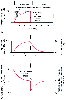Figure 17-12 Artificial ventilation by intermittent application of constant pressure (square wave) followed by passive expiration. The pressure required to overcome airway resistance (hatched lines, A) and the airflow rate (of Equation 4, C) are proportional to one another and decrease exponentially (assuming that resistance to airflow is constant). The pressure required to overcome the elastic forces (height of the dashed line, A) and lung volume (B) are proportional to one another and increase exponentially. Values shown are typical for an anesthetized supine paralyzed patient: total dynamic compliance, 50 mL/cm H₂ O; pulmonary resistance, 3 cm H₂ O/L/sec; apparatus resistance, 7 cm H₂ O/L/sec; total resistance, 10 cm H₂ O/L/sec; time constant, 0.5 second. (Redrawn from Lumb AB: Artificial ventilation. In Lumb AB [ed]: Nunn's Applied Respiratory Physiology, 5th ed. London, Butterworths, 2000, p 590.)

692

Because only a finite time is available for alveolar filling and because alveolar filling occurs in an exponential manner, the degree of filling obviously depends on the duration of the inspiration. The rapidity of change in an exponential curve can be described by its time constant τ, which is the time required to complete 63% of an exponentially changing function if the total time allowed for the function change is unlimited (2τ = 87%, 3τ = 95%, and 4τ = 98%). For lung inflation, τ = CT × R; normally, CT = 0.1 L/cm H₂ O, R = 2.0 cm H₂ O/L/sec, τ = 0.2 second, and 3τ = 0.6 second.

When this equation is applied to individual alveolar units, the time taken to fill such a unit clearly increases as airway resistance increases. The time to fill an alveolar unit also increases as compliance increases because a greater volume of air will be transferred into a more compliant alveolus before the retractive force equals the applied pressure. The compliance of individual alveoli differs from top to bottom of the lung, and the resistance of individual airways varies widely depending on their length and caliber. Therefore, various time constants for inflation exist throughout the lung.

Pathways of Collateral Ventilation

Collateral ventilation is another nongravitational determinant of the distribution of ventilation. Four pathways of collateral ventilation are known. First, interalveolar communications (pores of Kohn) exist in most species; they may range from 8 to 50 per alveolus and may increase with age and with the development of obstructive lung disease. Their precise role has not been defined, but they probably function to prevent hypoxia in neighboring, but obstructed lung units. Second, distal bronchiolar toalveolar communications are known to exist (channels of Lambert), but their function in vivo is speculative (may be similar to the pores of Kohn). Third, respiratory bronchiole-to-terminal bronchiole connections have been found in adjacent lung segments (channels of Martin) in healthy dogs and in humans with lung disease. Fourth, interlobar connections exist; the functional characteristics of interlobar collateral ventilation through these connections have been described in dogs,^[75] and they have been observed in humans as well.^[76]

Work of Breathing

The pressure-volume characteristics of the lung also determine the work of breathing. Because

Work = Force × Distance
Force = Pressure × Area
Distance = Volume/Area (7)

work is defined by the equation

Work = (Pressure × Area)(Volume/Area)
Work = Pressure × Volume (8)

and ventilatory work may be analyzed by plotting pressure against volume.^[77] In the presence of increased airway resistance or decreased CL, increased transpulmonary pressure is required to achieve a given VT with a consequent increase in the work of breathing. The metabolic cost of the work of breathing at rest constitutes only 1% to 3% of the total O₂ consumption in healthy subjects, but it is increased considerably (up to 50%) in patients with pulmonary disease.

Two different pressure-volume diagrams are shown in Figure 17-13 . During normal inspiration (left graph), transpulmonary pressure increases from 0 to 5 cm H₂ O while 500 mL of air is drawn into the lung. Potential energy is stored by the lung during inspiration and is expended during expiration; as a consequence, the entire expiratory cycle is passive. The hatched area plus the triangular area ABC represents pressure multiplied by volume and is the work of breathing. Line AB is the lower section of the pressure-volume curve of Figure 17-13 . The triangular area ABC is the work required to overcome elastic forces (CT), whereas the hatched area is the work required to overcome airflow or frictional resistance (R). The graph on the right applies to an anesthetized patient with diffuse obstructive airway disease resulting from the accumulation of mucous secretions. There is a marked

Figure 17-13 Lung volume plotted against transpulmonary pressure in a pressure-volume diagram for an healthy awake (normal) and an anesthetized patient. The lung compliance of the awake patient (slope of line AB = 100 mL/cm H₂ O) equals that shown for the small dependent alveoli in Figure 17-3 . The lung compliance of the anesthetized patient (slope of line AB' = 50 mL/cm H₂ O) equals that shown for the medium midlung alveoli in Figure 17-3 and for the anesthetized patient in Figure 17-12 . The total area within the oval and triangles has the dimensions of pressure multiplied by volume and represents the total work of breathing. The hatched area to the right of lines AB and AB' represents the active inspiratory work necessary to overcome resistance to airflow during inspiration (INSP). The hatched area to the left of the triangle AB'C represents the active expiratory work necessary to overcome resistance to airflow during expiration (EXP). Expiration is passive in the healthy subject because sufficient potential energy is stored during inspiration to produce expiratory airflow. The fraction of total inspiratory work necessary to overcome elastic resistance is shown by the triangles ABC and AB'C. The anesthetized patient has decreased compliance and increased elastic resistance work (triangle AB'C) when compared with the healthy patient's compliance and elastic resistance work (triangle ABC). The anesthetized patient shown in this figure has increased airway resistance to both inspiratory and expiratory work.

693

Figure 17-14 The diagrams show the work done against elastic and airflow resistance separately and summated to indicate the total work of breathing at different respiratory frequencies. The total work of breathing has a minimum value at about 15 breaths/min under normal circumstances. For the same minute volume, minimum work is performed at higher frequencies with stiff (less compliant) lungs and at lower frequencies when airflow resistance is increased. (Redrawn with modification from Lumb AB: Pulmonary ventilation: Mechanisms and the work of breathing. In Lumb AB [ed]: Nunn's Applied Respiratory Physiology, 5th ed. London, Butterworths, 2000, p 128.)

For a constant minute volume, the work done against elastic resistance is increased when breathing is deep and slow. On the other hand, the work done against airflow resistance is increased when breathing is rapid and shallow. If the two components are summated and the total work is plotted against respiratory frequency, there is an optimal respiratory frequency at which the total work of breathing is minimal ( Fig. 17-14 ).^[78] In patients with diseased lungs in which elastic resistance is high (pulmonary fibrosis, pulmonary edema, infants), the optimum frequency is increased, and rapid, shallow

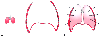Figure 17-15 A, The resting state of normal lungs when they are removed from the chest cavity; that is, elastic recoil causes total collapse. B, The resting state of a normal chest wall and diaphragm when the thoracic apex is open to the atmosphere and the thoracic contents are removed. C, The lung volume that exists at the end of expiration is the functional residual capacity (FRC). At FRC, the elastic forces of the lung and chest walls are equal and in opposite directions. The pleural surfaces link these two opposing forces. (Redrawn with modification from Shapiro BA, Harrison RA, Trout CA: The mechanics of ventilation. In Clinical Application of Respiratory Care, 3rd ed. Chicago, Year Book, 1985, p 57.)

Lung Volumes, Functional Residual Capacity, and Closing Capacity

Lung Volumes and Functional Residual Capacity

FRC is defined as the volume of gas in the lung at the end of a normal expiration when there is no airflow and PA equals ambient pressure. Under these conditions, expansive chest wall elastic forces are exactly balanced by retractive lung tissue elastic forces ( Fig. 17-15 ).^[80]

694

Figure 17-16 The dynamic lung volumes that can be measured by simple spirometry are tidal volume, inspiratory reserve volume, expiratory reserve volume, inspiratory capacity, and vital capacity. The static lung volumes are residual volume, functional residual capacity, and total lung capacity. Static lung volumes cannot be measured by simple spirometry and require separate methods of measurement (e.g., inert gas dilution, nitrogen washout, or whole-body plethysmography).

The expiratory reserve volume is part of FRC; it is that additional gas beyond the end-tidal volume that can be consciously exhaled and result in the minimum volume of lung possible, known as residual volume. Thus, FRC equals residual volume plus the expiratory reserve volume ( Fig. 17-16 ). With regard to the other lung volumes shown in Figure 17-16 , VT, vital capacity, inspiratory capacity, inspiratory reserve volume, and expiratory reserve volume can all be measured by simple spirometry. Total lung capacity (TLC), FRC, and residual volume all contain a fraction (residual volume) that cannot be measured by simple spirometry. However, if one of these three volumes is measured, the others can easily be derived because the other lung volumes, which relate these three volumes to one another, can be measured by simple spirometry.

Residual volume, FRC, and TLC can be measured by any of three techniques: (1) nitrogen washout, (2) inert gas dilution, and (3) total-body plethysmography. The first method, the nitrogen washout technique, is based on measuring expired nitrogen concentrations before and after breathing pure O₂ for several minutes and thus calculating the total quantity of nitrogen eliminated. Thus, if 2 L of nitrogen is eliminated and the initial alveolar nitrogen concentration was 80%, the initial volume of the lung was 2.5 L. The second method, the inert gas dilution technique, uses the wash-in of an inert tracer gas such as helium. If 50 mL of helium is introduced into the lungs and, after equilibration, the helium concentration is found to be 1%, the volume of the lung is 5 L. The third method, the total-body plethysmography technique, uses Boyle's law (i.e., P₁ V₁ = P₂ V₂ ), where P₁ = initial pressure, V₁ = initial volume). The subject is confined within a gas-tight box (plethysmograph) so that changes in the volume of the body during respiration may be readily determined as a change in pressure within the sealed box. Although each technique has technical limitations, all are based on sound physical and physiologic principles and provide accurate results in normal patients. Disparity between FRC as measured in the body plethysmograph and by the helium dilution method is often used as a way of detecting large, nonventilating air-trapped blebs.^[81] Obviously, there are difficulties in applying the body plethysmograph to anesthetized patients.

Airway Closure and Closing Capacity

As discussed earlier in the section on the distribution of ventilation, Ppl increases from the top to the bottom of the lung and determines regional alveolar size, compliance, and ventilation. Of even greater importance to the anesthesiologist is the recognition that these gradients in Ppl may lead to airway closure and collapse of alveoli.

AIRWAY CLOSURE IN PATIENTS WITH NORMAL LUNGS.

Figure 17-17A illustrates the normal resting end-expiratory (FRC) position of the lung-chest wall combination. The distending transpulmonary and the intrathoracic air passage transmural ΔP is 5 cm H₂ O, and the airways remain patent. During the middle of a normal inspiration ( Fig. 17-17B ), there is an increase in transmural ΔP (to 6.8 cm H₂ O) that encourages distention of the intrathoracic air passages. During the middle of a normal expiration ( Fig. 17-17C ), expiration is passive; PA is attributable only to the elastic recoil of the lung (2 cm H₂ O), and there is a decrease (to 5.2 cm H₂ O), but still a favorable (distending) intraluminal transmural ΔP. During the middle of a severe forced expiration ( Fig. 17-17D ), Ppl increases far higher than atmospheric pressure and is communicated to the alveoli, which have a pressure that is still higher because of the elastic recoil of the alveolar septa (an additional 2 cm H₂ O). At high gas flow rates, the pressure drop down the air passage is increased, and there will be a point at which intraluminal pressure equals either the surrounding parenchymal pressure or Ppl; that point is termed the equal pressure point (EPP). If the EPP occurs in small intrathoracic air passages (distal to the 11th generation, the airways have no cartilage and are called bronchioles), they may be held open at that particular point by the tethering effect of the elastic recoil of the immediately adjacent or surrounding lung parenchyma. If the EPP occurs in large extrathoracic air passages (proximal to the

695

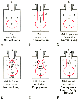Figure 17-17 Pressure gradients across the airways. The airways consist of a thin-walled intrathoracic portion (near the alveoli) and a more rigid (cartilaginous) intrathoracic and extrathoracic portion. During expiration, the pressure from elastic recoil is assumed to be +2 cm H₂ O in normal lungs (A–D) and +1 cm H₂ O in abnormal lungs (E and F). The total pressure inside the alveolus is pleural pressure plus elastic recoil. The arrows indicate the direction of airflow. EPP, equal pressure point. See the text for an explanation. (Redrawn with modification from Benumof JL: Anesthesia for Thoracic Surgery, 2nd ed. Philadelphia, WB Saunders, 1995, Chapter 8.)

In adults with normal lungs, airway closure may still occur even if exhalation is not forced, provided that residual volume is approached closely enough. Even in patients with normal lungs, as lung volume decreases toward residual volume during expiration, small airways (0.5 to 0.9 mm in diameter) show a progressive tendency to close, whereas larger airways remain patent.^{[83] [84]} Airway closure occurs first in the dependent lung regions (as directly observed by computed tomography)^[85] because the distending transpulmonary pressure is less and the volume change during expiration is greater. Airway closure is most likely to occur in the dependent regions of the lung whether the patient is in the supine or the lateral decubitus position ^[85] and whether ventilation is spontaneous or positive-pressure ventilation.^{[86] [87]}

AIRWAY CLOSURE IN PATIENTS WITH ABNORMAL LUNGS.

Airway closure occurs with milder active expiration, lower gas flow rates, and higher lung volumes and occurs closer to the alveolus in patients with emphysema, bronchitis, asthma, and pulmonary interstitial edema. In all four conditions, the increased airway resistance causes a larger decrease in pressure from the alveoli to the larger bronchi, thereby creating the potential for negative intrathoracic transmural ΔP and narrowed and collapsed airways. In addition, the structural integrity of the conducting airways may be diminished because of inflammation and scarring, and therefore these airways may close more readily for any given lung volume or transluminal ΔP.

In emphysema, the elastic recoil of the lung is reduced (to 1 cm H₂ O in Fig. 17-17E ), the air passages are poorly supported by the lung parenchyma, the point of airway resistance is close to the alveolus, and transmural ΔP can become negative quickly. Therefore, during only a mild forced expiration in an emphysematous patient, the EPP and the point of collapse are near the alveolus (see Fig. 17-17E ). The use of pursed-lip or grunting expiration (the equivalents of partly closing the larynx during expiration), PEEP, and continuous positive airway pressure in an emphysematous patient restores a favorable (distending) intrathoracic transmural air ΔP ( Fig. 17-17F ). In bronchitis, the airways are structurally weakened and may close when only a small negative transmural ΔP is present (as with mild forced expiration). In asthma, the middle-sized airways are narrowed by bronchospasm, and if expiration is forced, they are further narrowed by a negative transmural ΔP. Finally, with pulmonary interstitial edema, perialveolar interstitial edema compresses the alveoli and acutely decreases FRC; the peribronchial edema fluid cuffs (within the connective tissue sheaths around the larger arteries and bronchi) compress the bronchi and acutely increase closing volume.^{[88] [89] [90]}

MEASUREMENT OF CLOSING CAPACITY.

CC is a sensitive test of early small-airway disease and is performed by having the patient exhale to residual volume ( Fig. 17-18 ).^[91] As inhalation from residual volume toward TLC is begun, a bolus of tracer gas (xenon 133, helium) is injected into the inspired gas. During the initial part of this inhalation from residual volume, the first gas to enter the alveolus is the VD gas and the tracer bolus. The tracer gas will enter only alveoli that are already open (presumably the apices of the lung) and does not enter alveoli that are already closed (presumably the bases of the lung). As the inhalation continues, the apical alveoli complete filling and the basilar alveoli begin to open and fill, but with gas that does not contain any tracer gas.

696

Figure 17-18 Measurement of closing capacity with the use of a tracer gas such as xenon 133 (¹³³ Xe). The bolus of tracer gas is inhaled near residual volume and, because of airway closure in the dependent lung, is distributed only to nondependent alveoli whose air passages are still open (shown as crosshatched in diagram). During expiration, the concentration of tracer gas becomes constant after the dead space is washed out. This plateau (phase 3) gives way to a rising concentration of tracer gas (phase 4) when there is once again closure of the dependent airways because the only contribution made to expired gas is by the nondependent alveoli with a high ¹³³ Xe concentration. CC, closing capacity; FRC, functional residual volume; RV, residual volume; TLC, total lung capacity. (Redrawn with modification from Lumb AB: Respiratory system resistance: Measurement of closing capacity. In Lumb AB [ed]: Nunn's Applied Respiratory Physiology, 5th ed. London, Butterworths, 2000, p 79.)

A differential tracer gas concentration is thus established, with the gas in the apices having a higher tracer concentration (see Fig. 17-18 ) than that in the bases (see Fig. 17-18 ). As the subject exhales and the diaphragm ascends, a point is reached at which the small airways just above the diaphragm start to close and thereby limit airflow from these areas. The airflow now comes more from the upper lung fields, where the alveolar gas has a much higher tracer concentration, which results in a sudden increase in the tracer gas concentration toward the end of exhalation (phase IV of Fig. 17-18 ).

Closing volume (CV) is the difference between the onset of phase IV and residual volume; because it represents part of a vital capacity maneuver, it is expressed as a percentage of vital lung capacity. CV plus residual volume is known as CC and is expressed as a percentage of TLC. Smoking, obesity, aging, and the supine position increase CC.^[92] In healthy individuals at a mean age of 44 years, CC = FRC in the supine position, and at a mean age of 66 years, CC = FRC in the upright position.^[93]

RELATIONSHIP BETWEEN FUNCTIONAL RESIDUAL CAPACITY AND CLOSING CAPACITY.

The relationship between FRC and CC is far more important than consideration of FRC or CC alone because it is this relationship that determines whether a given respiratory unit is normal or atelectatic or has a low V̇A/ ratio. The relationship between FRC and CC is as follows. When the volume of the lung at which some airways close is greater than the whole of VT, lung volume never increases enough during tidal inspiration to open any of these airways. Thus, these airways stay closed during the entire tidal respiration. Airways that are closed all the time are equivalent to atelectasis ( Fig. 17-19 ). If the CV of some airways lies within VT, then as lung volume increases during inspiration, some previously closed airways will open for a short time until lung volume recedes once again below the CV of these airways. Because these opening and closing airways are open for a shorter time than normal airways are, they have less chance or time to participate in fresh gas exchange, a circumstance equivalent to a low-V̇A/ region. If the CC of the lung is below the whole of tidal respiration, no airways are closed at any time during tidal respiration; this is a normal circumstance. Anything that decreases FRC relative to CC or increases CC relative to FRC will convert normal areas to low-V̇A/ and atelectatic areas,^[94] which causes hypoxemia.

Mechanical intermittent positive-pressure breathing (IPPB) may be efficacious because it can take a previously spontaneously breathing patient with a low-V̇A/ relationship (in which CC is greater than FRC but still within VT, as depicted in Fig. 17-20, right panel ) and increase the amount of inspiratory time that some previously closed (at end-exhalation) airways spend in fresh gas exchange and thereby increase the V̇A/ relationship ( Fig. 17-20, middle panel ). However, if PEEP is added to IPPB, PEEP increases FRC to or above a lung volume greater than CC,

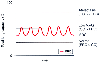Figure 17-19 Relationship between functional residual capacity (FRC) and closing capacity (CC). FRC is the amount of gas in the lungs at end-exhalation during normal tidal breathing, shown by the level of each trough of the sine wave tidal volume. CC is the amount of gas that must be in the lungs to keep the small conducting airways open. This figure shows three different CCs, as indicated by the three different straight lines. See the text for an explanation of why the three different FRC-CC relationships depicted result in normal or low ventilation-perfusion (V̇A/) relationships or atelectasis. The abscissa is time. (Redrawn from Benumof JL: Anesthesia for Thoracic Surgery, 2nd ed. Philadelphia, WB Saunders, 1995, Chapter 8.)

697

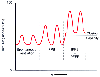Figure 17-20 Relationship of functional residual capacity (FRC) to closing capacity (CC) during spontaneous ventilation, intermittent positive-pressure breathing (IPPB), and IPPB and positive end-expiratory pressure (IPPB + PEEP). See the text for an explanation of the effect of the two ventilatory maneuvers (IPPB and PEEP) on the relationship of FRC to CC. TLC, total lung capacity. The abscissa is time.