Book Text

Dynamic Pressure Measurement (Transducer)

Accurate measurement of a rapidly changing pressure, such as arterial blood pressure, is more difficult and complex. There are many characteristics of the pressure-versus-time waveform that we might wish to determine. Systolic, diastolic, and mean arterial pressure is given by the maximum, minimum, and average pressure values during the cardiac cycle ( Fig. 30-12 ). In addition, we can measure the maximum upward slope of the waveform

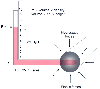Figure 30-11 Manometer. A water manometer uses a balance of forces. In this case, downward pressure of the fluid, as determined by its density and height, balances the upward pressure of the central venous system caused by hydrostatic and elastic recoil forces.

during systole, which is related to the speed of ventricular ejection. An abnormally rapid downslope after aortic valve closure (indicated by the dicrotic notch) suggests possible aortic insufficiency. Thus, the details of the pressure-time waveform, as well as its maxima and minima, are potentially important to the clinician.

A modern pressure transducer is a device that changes either electrical resistance or capacitance in response to changes in pressure on a solid-state device. The variable transducer resistance is placed in an electrical circuit involving three known resistances (Wheatstone bridge; see Appendix 3 ), and the change in resistance is converted into electrical voltage. The moving part of the

Figure 30-12 Arterial waveform. Systolic pressure is defined as the instantaneous maximal pressure; diastolic, the instantaneous minimal pressure; and mean, the average pressure over a cycle. dP/dT refers to the upstroke of the arterial pressure, that is, the rate of pressure generation. Mean pressure is estimated as diastolic plus one third the pulse pressure (systolic — diastolic) when only systolic and diastolic pressure is known.

1200

transducer itself is very small and has little mass. However, it is not clinically or commercially practical to place the transducer in contact with arterial blood, so we use a liquid-filled tube to connect the intra-arterial catheter to the pressure transducer. This system of a fluctuating driving pressure (i.e., the arterial pressure being measured), a liquid-filled tube, and a pressure transducer is mechanically equivalent to the mass-spring harmonic oscillator shown in Figure 30-13 . The mass (m) represents the mass of the fluid in the tubing. The spring represents the elasticity of the tubing. The damper, shown schematically as a piston moving in oil, represents the friction generated by the fluid moving to and fro in the tubing.

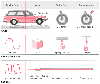Figure 30-13 A to C, Damping and resonance. Pressure measured in an invasive arterial catheter can actually overshoot or amplify the real blood pressure. This phenomenon is referred to as the dynamic frequency response of the fluid-filled arterial line and transducer system. The phenomenon has a physical model that can generate an equation to predict the output pressure response, depending on the frequency of the input pressure and several physical parameters of the system. In the physical model on the right, driving pressure (arterial blood pressure) acts on a mass (the fluid within the arterial pressure tubing) by pushing it up and down against a spring, which stores energy (the compliant pressure tubing), and on a dash pot, which opposes motion in either direction (the resistance of the fluid as it moves to and fro within the pressure tubing). Depending on the input frequency, the output may undergo amplification as it reaches a specific frequency, known as the resonant frequency of the system. On the left side of the figure is a common phenomenon noted when a car drives along a bumpy dirt road. In this situation, the driving force is the bumps in the road, which act on the tire. The car spring is equivalent to compliance to the pressure tubing, and the shock absorber corresponds to the resistance of fluid moving back and forth in the arterial line. The mass of the fluid is analogous to the mass of the front of the car. You may have experienced the phenomenon: when you reach a certain speed as you are driving along a bumpy road, the front of the car starts to oscillate with increasing amplitude. If you speed up or slow down, this phenomenon disappears. The car bounces highest when you have reached the resonant frequency of this harmonic oscillator. See Appendix 4 for a detailed mathematical description of this process.

A more commonly encountered harmonic oscillator is that of a car driving down a bumpy dirt road (see Fig. 30-13 ). In this case, the oscillating driving pressure is provided by the bumps in the road, which force the car wheel to oscillate up and down. The car springs are analogous to the compliance of the arterial pressure tubing, and the car's shock absorbers, which oppose motion of the wheel in either direction, are analogous to the friction of the fluid moving back and forth in the fluid-filled tube. Depending on the frequency of the bumps (i.e., driving pressure frequency), the system can either suppress the bumpy road or may initiate dramatically increased oscillations. The frequency of the driving force that causes maximal amplification of the signal is called the natural

1201

resonant frequency ( Fig. 30-14 ). The degree of amplification is directly related to the mass and inversely related to the amount of friction present; for large amounts of friction, attenuation rather than amplification occurs (see Appendix 4 ).

To visualize this concept intuitively, hang a weight on the end of a rubber band while holding the upper end of the band in your hand. If you move your hand up and down slowly, the weight follows your hand movements almost exactly. As you increase the frequency of your hand oscillations, the weight begins to "lag" behind your hand, and the amplitude of the weight movement begins to increase. As you approach the natural frequency of this simple system, you will observe the phenomenon of "resonance" when the amplitude of the weight motion becomes very large. If you try different rubber bands and weights, you will find that stiffer bands or smaller weights yield higher natural frequencies. The same is true of our fluid-coupled pressure transducer system. Stiffer (i.e., less compliant) tubing or a shorter length of tubing (less mass) produces higher natural frequencies in this system; that is, it requires a much higher pulse rate before amplification.

To minimize the potential of amplification of the real arterial pressure, the system should have very noncompliant (i.e., stiff) tubing and the total mass of liquid in the system should also be minimized, which can be accomplished by having small-diameter tubing and as short a length as possible. In most clinical systems, the natural resonant frequency is 10 to 15 Hz, which is much higher than the primary frequency of the arterial waveform (the heart rate is 60 to 120 beats/min or 1 to 2 Hz). Unfortunately, the arterial waveform is not a sine wave, but is the more complex shape shown in Figure 30-6 and is made up of a summation of sine waves, a Fourier series. The higher-frequency components of the arterial waveform (higher harmonics) are the ones that are closer to the natural frequency and are therefore amplified. This is

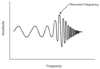Figure 30-14 Amplitude and frequency. As the frequency increases, the amplification can increase to a maximum, and then the signal becomes attenuated. (Adapted from Sykes MK, Vickers MD, Hull CJ: Principles of Measurement and Monitoring in Anaesthesia and Intensive Care, 3rd ed. Oxford, Blackwell, 1991.)

why we see a "whip" in the waveform when the peak systolic pressure and the initial upstroke are amplified significantly above the true systolic pressure, even if the heart rate itself is not in the range of the resonant frequency. In theory, mean arterial pressure should be the same because this amplification of systolic pressure also produces a reduction in diastolic pressure (see Appendix 4 ).

These fast-responding pressure transducers are often used to measure both central venous pressure and pulmonary artery pressure. As such, they have a frequency response much greater than necessary to faithfully reproduce the actual signal. However, the clinical meaning and interpretation of measurements from pulmonary artery catheters have been under scrutiny for years.^[6] A recent study^[7] has shown no definitive benefit in patient outcomes from the use of pulmonary artery catheters. These "problems" with pulmonary artery catheters are not the result of physical flaws in the catheter or the transducer, but reside within the meaning of the information that we extract from the data.