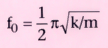APPENDIX 4: Amplification Artifact of a Fluid Tube/Transducer Pressure Wave

The amplification artifact of a fluid tube/transducer pressure waveform can be calculated if a few properties of the system are known. The most relevant part of this solution is the response amplitude, which is plotted against the driving frequency (f) in Figure 30-14 . This figure shows some important properties of fluid-coupled transducers and other harmonic oscillators. One of these properties is the existence of a resonant frequency, f₀ , which is defined as follows:





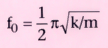
Remember, m is the mass of the system and k is the elasticity, or spring constant.

As we increase the amount of damping (i.e., friction; c is the friction constant), we observe a decrease in the peak amplitude at resonance, and the frequency at which the peak occurs decreases slightly. The damping coefficient (z) is defined as follows:





Even though the arterial pressure waveform is not actually sinusoidal, Figure 30-14 shows the most important characteristics of the pressure transducer response. Any combination of catheter, tubing, and transducer can be characterized by two quantities: a resonant frequency (f₀ ) and a damping coefficient (z). Gardner measured these quantities for many transducer and tubing systems and found that most systems have resonant frequencies of 10 to 20 cycles/sec

1221

If the resonant frequency is 10 Hz (600 cycles/min), one might conclude that amplification plays little role in the clinical range of pulse rates, which are 5 to 10 times smaller. However, the arterial pressure waveform is not a sine wave. It can be represented as a summation of sine waves (a Fourier series) with frequencies up to many times the pulse rate. It is these higher harmonic frequencies that are amplified most and that yield the spiked appearance of a poorly processed arterial waveform. Depending on the shape of the actual arterial pressure wave, this distortion can introduce a 20% to 40% "overshoot" error in systolic blood pressure readings. Even worse, this error is dependent on the pulse rate, so an error determined for a particular patient at the beginning of administration of an anesthetic may not remain constant.

From this discussion we can easily predict how to optimize the performance of a pressure transducer system. First, the resonant frequency (f₀ ) should be as high as possible. Therefore, the value for k in Equation 1 should be large (i.e., the spring should be "stiff"), and the value for m should be small (i.e., the cannula and pressure tubing should be as stiff and inelastic as possible). To minimize the mass of the moving fluid, the tubing should be short in length and small in diameter. Judging from plots of amplitude versus frequency/resonant frequency at different damping coefficients, the optimal damping coefficient would be 0.4 to 0.5. One should also carefully eliminate air bubbles from the system because they add elasticity and friction, thereby lowering the resonant frequency. In a clinical system, one can determine the approximate f₀ and z of a transducer system if graphic output is available. If the high-pressure flush is turned on and then quickly off at a high chart speed (50 mm/sec), the tracing oscillates through several cycles at a frequency near f₀ . The damping coefficient can be found by determining the ratio of amplitudes of successive peaks on the tracing. This is a practical example of how fundamental principles of mechanics can be used to predict and optimize the performance of monitoring systems. These concepts of mechanics will recur in later sections of this chapter.