|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Many of our monitors are based on fundamental principles of the mechanics of solids and fluids, usually a derivation of F = ma. We discuss a few of these principles in this section and provide common examples of each.
Many of our monitors measure force, which is related to mass and
acceleration as described by Equation 1, Newton's second law. The force may be generated
by gravity, a beating heart, a compressed gas, or a contracting muscle. When we
weigh a patient, we are determining the force exerted by gravity at the earth's surface
on the patient's mass (m). This gravitational force (Fg
) is related to
mass by the formula
Fg
= mg (2)
where g, the gravitational constant for acceleration, equals 9.8 N/kg ( Fig.
30-9
). Many anesthetic monitors measure pressure, which is force divided
by the area of the surface on which that force is exerted. Pressure thus has dimensions
of force/area, and its SI unit is the newton/meter2
, which is called the
pascal. Because the pascal is a very small unit
of pressure, we usually choose to use kilopascal,
which equals 1000 Pa.
As noted earlier, kinetic energy is proportional to mass times velocity squared and is measured in kg-m2 /sec2 , or joules.
Figure 30-6
Fourier series. This pseudoarterial waveform was generated
by adding the three sine waves with the following characteristics: y = 50 sin x,
y = 25 sin 2x, y = 12 sin 4x.
If a force (F) acts on a mass (m) over a distance (d), we define
work as the product of the force and distance: W
= Fd. It can be shown from Equation 1 (using a little calculus; see Appendix
1
at the end of this chapter) that the work performed on a mass equals
the change in its kinetic energy:
W = Fd = Δ½(mv2
) (3)
Work has dimensions of force times distance and SI units of newton-meters. Because work and energy change are equivalent, 1 N-m must equal 1 kg-m2 /sec2 = 1 joule (J). This equivalence of units can be verified by Equation 1.
Figure 30-7
Spectral arrays. A compressed spectral array can display
the frequency on the x axis and power on the y
axis. A number of these arrays can be aligned with time as a third axis to give
an indication of changes in power over time.
Figure 30-8
Advanced signal processing. After a signal has been
transduced (see Fig. 30-3
)
and initially processed (see Fig.
30-4
, Fig. 30-5
,
Fig. 30-6
, and Fig.
30-7
), it can then be further analyzed, converted into data streams for
transfer and storage, encoded for security, and linked to other signals for presentation
to the user as information.
The relationship of work and energy leads to the concept of potential
energy. If we lift mass (m) by a height (z) above the floor and let it
fall, the force of gravity (Fg
= mg) acts on the mass through the distance
(z), thus doing work:
W = Fd = mgz (4)
At the end of its fall, the mass has a kinetic energy equal to the work performed, mgz (Equation 3). Therefore, we say that when the mass is raised to the height z above the floor, we have given it a potential energy equal to mgz. A 1-kg mass lifted 1 m off the floor has a potential energy of 9.8 J. This potential energy can be converted into the kinetic energy of motion simply by letting the mass fall. Potential energy can be stored in many other forms besides height (called "gravitational potential"), for example, a compressed spring, gas at high pressure in a tank, or the electrical potential of a battery ( Fig. 30-10 ).
Energy is related to matter in one additional way through Einstein's famous equation E = mc2 . That is to say, matter and energy are the same "stuff." In the absolute sense, usually reserved for thermonuclear weapons, atomic reactors, and the sun, matter can be converted into energy,
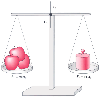Figure 30-9
Balance. A scale is in balance when the forces are equal
and in opposite directions. The force of gravity on the unknown mass of fruit is
balanced by the known standard masses on the opposite side of the balance. F1
= F2
, and hence m1
ag
= m2
ag
;
because ag
= ag
, m1
= m2
. ag
,
acceleration caused by gravity.
We have already defined power as the rate of change in energy per unit time. With the additional relationship between work and energy (Equation 3), it is clear that power is also the "rate of work," or the amount of work performed per unit time. Thus, the unit of power (1 W = 1 J/sec) can also be expressed as the newton-meter/second.
|
|
|
|
|
|
|
|
|
|
|
|
|
