|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Some physiologic values are constant over time, whereas others vary. When a measured value changes over time, it constitutes a signal. Many physiologic processes generate signals that cannot be perceived by our senses or are too small to measure directly. We must process and amplify these signals, a situation that introduces new problems. The first step in processing is to convert the raw physiologic variable (e.g., pressure, temperature, velocity) into
 Figure 30-2
Accuracy and precision. The bias plot is a way to compare
two different methods of measuring the same variable. Examples are plotted above
on the right for saturation values, blood analysis versus pulse oximetry. It is
a plot of the difference between the two measurements being compared versus the average
of those two measurements. If one method constantly measures slightly higher than
the other by a consistent value, it has a positive bias. If it has only slight variation
around that bias, it is said to have very low random error (or precision, which equals
the standard deviation of the differences) (A). B,
The values are randomly scattered such that the average difference is near zero,
but the precision value is very large. This large random error makes the device
unusable because calibration will not improve this random error. C,
The optimal device, that is, a bias near zero and a very small precision (standard
deviation of the differences). No amount of calibrating or "sighting in" could cause
B to become more accurate because the error is randomly
scattered.
Figure 30-2
Accuracy and precision. The bias plot is a way to compare
two different methods of measuring the same variable. Examples are plotted above
on the right for saturation values, blood analysis versus pulse oximetry. It is
a plot of the difference between the two measurements being compared versus the average
of those two measurements. If one method constantly measures slightly higher than
the other by a consistent value, it has a positive bias. If it has only slight variation
around that bias, it is said to have very low random error (or precision, which equals
the standard deviation of the differences) (A). B,
The values are randomly scattered such that the average difference is near zero,
but the precision value is very large. This large random error makes the device
unusable because calibration will not improve this random error. C,
The optimal device, that is, a bias near zero and a very small precision (standard
deviation of the differences). No amount of calibrating or "sighting in" could cause
B to become more accurate because the error is randomly
scattered.
When an analog signal (e.g., voltage versus time) is amplified, both the background noise and the desired signal are amplified ( Fig. 30-4 ). Various techniques can be used to enhance the signal-to-noise ratio. For instance, most pulse oximeters assume that a patient's pulse rate is between 30 and 300 beats per minute. Therefore, the instrument filters out any pulsations that occur at frequencies below 30 or above 300 (see the section on alternating current, capacitors, and impedance). In some cases, a desired signal can be repeated and summated, and the accompanying random noise becomes a smaller fraction of the signal. Evoked potentials are an excellent example of this process. The evoked response signal for a single stimulus is actually much smaller than the random noise, but this signal is nearly identical after each stimulus. Therefore, by summing the potentials after many stimuli, we reinforce the evoked response signal but not the noise ( Fig. 30-5 ).
Finally, the waveform of any periodic signal can be represented by a summation of sinusoidal waves, called a "Fourier series" ( Fig. 30-6 ).[3] The component sine waves can be described by their frequency and amplitude (or power, which is proportional to the square of the amplitude). Thus, a waveform originally expressed as amplitude versus time is transformed into a plot of power versus frequency ( Fig. 30-7 ). The resulting plot, called the "power spectrum," is a common form for displaying and interpreting some types of waveform data, such as the electroencephalogram (see Chapter 38 ).
When we monitor a patient, we measure physical quantities in a physiologic setting, and these measurements are subject to error and uncertainty. Our task as anesthesiologists is to understand both the physiologic and the physical limitations of these measurements, judge the potential for error, and make clinical decisions in the face of these uncertainties.
A new form of signal analysis has entered the realm of anesthesiology. Our recording of vital signs and patient data, first begun a century ago by Harvey Cushing,[4] is a primitive form of signal analysis. To quote Dr. Cushing[5] :
In all serious or questionable cases the patient's pulse and blood-pressure, their usual rate and level having been previously taken under normal ward conditions, should be followed throughout the entire procedure, and the observations recorded on a plotted chart. Only in this way can we gain any idea of physiological disturbances—whether given manipulations are leading to shock, whether there is a fall of blood-pressure from loss of blood, whether the slowed pulse is due to compression, and so on.
The singal, whether an observed pupillary sign, palpated pulse, transduced pressure, or auscultated breath sound, was integrated by the anesthetist, interpreted (is this real or is it artifact?), and charted (data storage). Modern data recorders use the same principles. Additionally, data storage has become much more complex. Not only must the signal be transduced, but it must also be recorded, either in raw or in processed form ( Fig. 30-8 ). This point is important because it introduces new possibilities in monitoring (trends, signals, feedback to user) and new pitfalls. Imagine an anesthesia record that would alert you to future potential physiologic issues from currently monitored data and predictive algorithms, that is, an intelligent anesthesia record. New problems are introduced
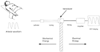 Figure 30-3
Transducer. A transducer changes a signal from one form
of energy to another. A common transducer in anesthesia changes mechanical energy,
such as an arterial pulse, into electrical energy. Microphones and speakers are
also examples of transducers.
Figure 30-3
Transducer. A transducer changes a signal from one form
of energy to another. A common transducer in anesthesia changes mechanical energy,
such as an arterial pulse, into electrical energy. Microphones and speakers are
also examples of transducers.
 Figure 30-4
Digital and analog signal processing. The analog signal
shows distortion and loss of fidelity as it is reduced and then amplified. The digital
signal shows no such loss. To create the analog example, a copying machine was used
to shrink the text and then enlarge it. For the digital signal, the font size was
reduced, the text copied, and the process reversed.
Figure 30-4
Digital and analog signal processing. The analog signal
shows distortion and loss of fidelity as it is reduced and then amplified. The digital
signal shows no such loss. To create the analog example, a copying machine was used
to shrink the text and then enlarge it. For the digital signal, the font size was
reduced, the text copied, and the process reversed.
 Figure 30-5
Somatosensory evoked potentials. A background signal
can be separated from random noise by repeatedly adding the signals. The noise (random)
is equally likely to be positive or negative; hence, adding positive and negative
yields zero with multiple summations.
Figure 30-5
Somatosensory evoked potentials. A background signal
can be separated from random noise by repeatedly adding the signals. The noise (random)
is equally likely to be positive or negative; hence, adding positive and negative
yields zero with multiple summations.
|
|
|
|
|
|
|
|
|
|
|
|
|