Potency of Nondepolarizing Neuromuscular Blockers
Drug potency is commonly expressed by the dose-response relationship.
The dose of a neuromuscular blocking drug required to produce an effect (e.g., 50%,
90%, or 95% depression of twitch height; commonly expressed as ED50
,
TABLE 13-5 -- Dose-response relationships of nondepolarizing neuromuscular blocking drugs
in human subjects
|
ED50
(mg/kg) |
ED90
(mg/kg) |
ED95
(mg/kg) |
References |
|
Long Acting |
|
Pancuronium |
0.036 (0.022–0.042) |
0.056 (0.044–0.070) |
0.067 (0.059–0.080) |
[179]
[190]
|
|
Pipecuronium |
0.021 (0.013–0.032) |
0.032 (0.022–0.033) |
0.042 (0.024–0.059) |
[179]
[191]
[192]
[193]
[194]
[195]
[196]
|
|
d-Tubocurarine |
0.23 (0.16–0.26) |
0.41 (0.27–0.45) |
0.48 (0.34–0.56) |
[190]
|
|
Metocurine |
0.14 (0.13–0.15) |
0.25 (0.24–0.26) |
0.30 (0.28–0.32) |
[190]
|
|
Doxacurium |
0.012 (0.006–0.016) |
0.022 (0.021–0.024) |
0.024 (0.016–0.033) |
[197]
[198]
[199]
[200]
[201]
|
|
Gallamine |
1.30 |
2.30 |
2.82 |
[190]
|
|
Alcuronium |
0.11 (0.07–16) |
0.18 (0.12–0.25) |
0.22 (0.14–0.29) |
[190]
|
|
Intermediate Acting |
|
Rocuronium |
0.147 (0.069–0.220) |
0.268 (0.200–0.419) |
0.305 (0.257–0.521) |
[179]
[202]
[203]
[204]
[205]
[206]
[207]
[208]
|
|
Vecuronium |
0.027 (0.015–0.031) |
0.042 (0.023–0.055) |
0.043 (0.037–0.059) |
[190]
|
|
Atracurium |
0.12 (0.08–0.15) |
0.18 (0.19–0.24) |
0.21 (0.13–0.28) |
[190]
|
|
Cisatracurium |
0.026 (0.015–0.031) |
— |
0.04 (0.032–0.05) |
[209]
[210]
[211]
[212]
[213]
|
|
Short Acting |
|
Mivacurium |
0.039 (0.027–0.052) |
— |
0.067 (0.045–0.081) |
[10]
[214]
[215]
[216]
[217]
[218]
|
|
Rapacuronium |
0.39 |
— |
0.75–1.0 |
[219]
[220]
|
|
Ultrashort Acting |
|
430A |
0.09 |
— |
0.19 |
[188]
|
|
Data are the median and range of reported values. |
|
ED50
, ED90
, and ED95
, doses
of each drug that produce, respectively, a 50%, 90%, and 95% decrease in the force
of contraction or amplitude of the electromyogram of the adductor pollicis muscle
after ulnar nerve stimulation. |
Figure 13-13
Chemical structure of alcuronium, the semisynthetic diallyl
derivative of toxiferine. The quaternizing allyl groups actually reduce the potency
by a factor of 3 to 5.
ED90
, and ED95
, respectively) is taken as a measure of the
potency of neuromuscular blockers.[10]
[179]
[188]
[190]
[191]
[192]
[193]
[194]
[195]
[196]
[197]
[198]
[199]
[200]
[201]
[202]
[203]
[204]
[205]
[206]
[207]
[208]
[209]
[210]
[211]
[212]
[213]
[214]
[215]
[216]
[217]
[218]
[219]
[220]
The
drugs have different potencies as illustrated in Table
13-5
and Figure 13-14
.
For factors affecting the potency of neuromuscular blockers, see the section "Drug
Interactions." The dose-response relationship for nondepolarizing neuromuscular
blockers is sigmoidal in shape (see Fig.
13-14
) and has been derived in a variety of ways. The simplest method
is to perform linear regression over the approximately linear portion of a semilogarithmic
plot between 25% and 75% neuromuscular block. Alternatively, the curve can be subjected
to probit or logit transform to linearize it over its whole length or be subjected
to nonlinear regression with the sigmoid Emax model of the form:
Effect(e) = .\F(dosee
γ
,
dosee
γ
+ dosee50
γ
)
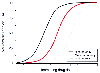Figure 13-14
Schematic representation of a semilogarithmic plot of
muscle relaxant dose versus neuromuscular block. A drug of high potency would be
represented by doxacurium, one of medium potency by atracurium, and one of low potency
by rocuronium. The graph illustrates that the relative potencies of the muscle relaxants
span a range of approximately 2 orders of magnitude.
This equation can be applied to the raw data.[221]
[222]
[223]
More
complex models that relate the concentration of neuromuscular blockers at the neuromuscular
junction to their pharmacologic effect have been developed, and they will be discussed
later.[224]
[225]
