Maintenance Infusion Rate
By definition, the rate at which drug exits the body is systemic
clearance, ClS
, times the plasma concentration. To maintain a given target
concentration, CT
, drug must be delivered at the same rate that drug is
exiting the body. Thus,
Maintenance infusion rate = CT
× ClS
(13)
For drugs with multicompartmental pharmacokinetics, which includes all the intravenous
drugs used in anesthetic practice, drug is distributed into peripheral tissues as
well as cleared from the body. The rate of distribution into tissues changes over
time as tissue levels equilibrate with plasma levels. Equation 13 is correct only
after the peripheral tissues have fully equilibrated with plasma, which requires
many hours. At all other times, this maintenance infusion rate underestimates the
infusion rate to maintain a target concentration.
In some situations, this simple maintenance rate calculation may
be acceptable. For example, if an infusion at this rate is used along with a bolus
dose based on Vdpe
and the drug has a long delay between the bolus and
peak effect, much of the distribution of drug into tissues may have occurred by the
time that the effect-site concentration reaches the target concentration. In this
case, the maintenance infusion rate calculated as clearance times target concentration
may be fairly accurate because Vdpe
is sufficiently higher than V1
to account for the distribution of drug into peripheral tissues. Unfortunately,
most drugs used in anesthesia have sufficiently rapid equilibration between plasma
and the effect site that Vdpe
does not adequately encompass the distribution
process, thus making this approach unsuitable.
Another example of calculating infusion rates for drugs with multicompartmental
pharmacokinetics is the two-step approach proposed by Wagner.[80]
In this method, two infusions, Q1
and Q2
, are administered
in sequence. The loading infusion, Q1
, is selected on the basis of convenience
and the degree of overshoot in plasma concentration that will be clinically acceptable.
The second infusion, Q2
, is calculated as CT
×
ClS
, exactly as noted earlier. The Wagner two-step approach
does not consider the time course of drug effect and thus is probably not appropriate
for most anesthetic drugs.
Having offered to the reader two approaches that do not work very
well, we now turn to approaches that are mathematically and clinically sound. Because
the net flow of drug into peripheral tissues decreases over time, the infusion rate
required to maintain any desired concentration must also decrease over time. If
the initial bolus has been based on Vdpe
, no infusion need be administered
until the effect-site concentrations peak. After the peak in effect-site concentration,
the (nearly) correct equation to maintain the desired concentration is
Maintenance infusion rate = CT
× V1
× (k10
+ k12
e−k21
t
+ k13
e−k31
t
)
(14)
This equation indicates that a high infusion rate is initially
required to maintain CT
. Over time, the infusion rate gradually decreases
(see Fig. 12-4
). At equilibrium
(t = ∞), the infusion rate decreases to CT
V1
k10
,
which is the same as CT
ClS
. Few anesthesiologists would choose
to mentally solve such an equation during administration of an
TABLE 12-3 -- Plasma drug concentration ranges
|
|
Stimulus |
|
|
|
|
Drug
*
|
Skin Incision |
Minor Surgery |
Major Surgery |
Spontaneous Ventilation |
Awakening |
Analgesia or Sedation |
|
Alfentanil (ng/mL) |
200–300 |
250–450 |
100–300 |
<200–250 |
— |
50–100 |
|
Fentanyl (ng/mL) |
3–6 |
4–8 |
2–5 |
<1–2 |
— |
1–2 |
|
Sufentanil (ng/mL) |
1–3 |
2–5 |
1–3 |
<0.2 |
— |
0.02–0.2 |
|
Remifentanil (ng/mL) |
4–8 |
4–8 |
2–4 |
<1–3 |
— |
1–2 |
|
Propofol (µg/mL) |
2–6 |
2.5–7.5 |
2–6 |
— |
0.8–1.8 |
1.0–3.0 |
|
Methohexital (µg/mL) |
5–10 |
5–15 |
5–10 |
— |
1–3 |
2–5 |
|
Thiopental (µg/mL) |
7.5–12.5 (with N2
O) 35–45 (without N2
O) |
10–20 |
10–20 |
— |
4–8 |
7.5–15.0 |
|
Etomidate (ng/mL) |
400–600 |
500–1000 |
300–600 |
— |
200–350 |
100–300 |
|
Midazolam (ng/mL) |
— |
50–250 (combined with an opioid) |
50–250 (combined with an opioid) |
— |
150–200 (reduced to 20–70 in the presence of an opioid) |
40–100 |
|
Ketamine (µg/mL) |
— |
— |
1–2 |
— |
— |
0.1–1 |
*Drug
levels are when combined with 65% to 70% nitrous oxide (N2
O) unless otherwise
stated. Effective plasma concentrations may differ markedly, depending on premedication
and intraoperative drug combinations.
anesthetic. Fortunately, some simple techniques can be used in place of solving
such a complex expression.
Figure 12-15
is a nomogram in which Equation 14 has been solved, and it shows the infusion rates
over time necessary to maintain any desired concentration of fentanyl, alfentanil,
sufentanil, and propofol. This nomogram is complex, so we will review it in detail.
The y axis represents the target concentration CT
.
The x axis is the time since the beginning of the
anesthetic (i.e., since the initial bolus). The suggested target initial concentrations
(shown in red) are based on the work of Vuyk and colleagues[40]
with propofol and alfentanil (see Fig.
12-8
) and are scaled to fentanyl and sufentanil based on their relative
potencies.[78]
The intersections of the target
concentration line and the diagonal lines indicate the infusion rate appropriate
at each point in time. For example, to maintain a fentanyl concentration of 1.5
ng/mL, the appropriate rates are 4.5 µg/kg/hr at 15 minutes, 3.6 µg/kg/hr
at 30 minutes, 2.7 µg/kg/hr at 60 minutes, 2.1 µg/kg/hr at 120 minutes,
and 1.5 µg/kg/hr at 180 minutes. Of course, you can select target concentrations
and different times of rate adjustment, depending on clinical circumstances
 Figure 12-14
Pharmacokinetic simulation demonstrating the limitations
of infusion regimens based on simple pharmacokinetic parameters, with fentanyl used
as an example. These infusion schemes were designed to achieve a plasma fentanyl
concentration of 3 ng/mL. The upper curve shows
that a regimen using a loading dose based on the volume of distribution followed
by a constant infusion based on clearance results in a transient period of extremely
high plasma concentrations. If the same maintenance infusion is given but the loading
dose is based on the volume of the central compartment, distribution of drug to the
peripheral compartments causes the plasma concentration to fall below the desired
level until the compartments reach steady-state concentrations, as shown in the lower
curve. Cp, plasma drug concentration.
Figure 12-14
Pharmacokinetic simulation demonstrating the limitations
of infusion regimens based on simple pharmacokinetic parameters, with fentanyl used
as an example. These infusion schemes were designed to achieve a plasma fentanyl
concentration of 3 ng/mL. The upper curve shows
that a regimen using a loading dose based on the volume of distribution followed
by a constant infusion based on clearance results in a transient period of extremely
high plasma concentrations. If the same maintenance infusion is given but the loading
dose is based on the volume of the central compartment, distribution of drug to the
peripheral compartments causes the plasma concentration to fall below the desired
level until the compartments reach steady-state concentrations, as shown in the lower
curve. Cp, plasma drug concentration.
and your assessment of how accurately the intravenous drug needs to be titrated.
Another recent approach to manually determining infusion rates
for maintenance of anesthesia to a desired target concentration is through the use
of concepts used with a slide rule.[81]
Figure
12-16
illustrates such a slide rule for propofol. As described by Bruhn
and coauthors, "The bolus dose required to reach a given target plasma concentration
is the product of the (weight-related) distribution volume
TABLE 12-4 -- Volume of distribution at the time of peak effect
|
Drug |
V1
(L) |
Vdpe
(L) |
|
Fentanyl |
12.7 |
75 |
|
Alfentanil |
2.19 |
5.9 |
|
Sufentanil |
17.8 |
89 |
|
Remifentanil |
5.0 |
17 |
|
Propofol |
6.7 |
37 |
|
Thiopental |
5.6 |
14.6 |
|
Midazolam |
3.4 |
31 |
|
V1
, volume of the central compartment; Vdpe
,
apparent volume of distribution at the time of peak effect. |
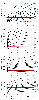 Figure 12-15
Nomogram for calculating maintenance infusion rates to
maintain a stable concentration of fentanyl, alfentanil, sufentanil, or propofol.
The y axis is the desired concentration. The x
axis is the time relative to the initial bolus. The diagonal
lines show the infusion rates at different times required to maintain
the desired concentration selected on the y axis.
Figure 12-15
Nomogram for calculating maintenance infusion rates to
maintain a stable concentration of fentanyl, alfentanil, sufentanil, or propofol.
The y axis is the desired concentration. The x
axis is the time relative to the initial bolus. The diagonal
lines show the infusion rates at different times required to maintain
the desired concentration selected on the y axis.
 Figure 12-16
Slide rule for calculating the maintenance propofol infusion
rate from the patient's weight, the desired target concentration, and the elapsed
time. (Adapted from Bruhn J, Bouillon TW, Ropcke H, Hoeft A: A manual slide
rule for target-controlled infusion of propofol: Development and evaluation. Anesth
Analg 96:142–147, 2003.)
Figure 12-16
Slide rule for calculating the maintenance propofol infusion
rate from the patient's weight, the desired target concentration, and the elapsed
time. (Adapted from Bruhn J, Bouillon TW, Ropcke H, Hoeft A: A manual slide
rule for target-controlled infusion of propofol: Development and evaluation. Anesth
Analg 96:142–147, 2003.)
and the required concentration. Similarly, the infusion rate at a particular time
point is the product of target concentration, body weight, and a correction factor
that depends on the time elapsed from the start of the initial infusion. This factor
can be determined for each time point by using a PK simulation program."[81]
When compared with computer simulation programs, this manual device performed within
an acceptable degree of accuracy (within 7% of the simulated target concentration)
for a single target concentration and decreased in accuracy (within 20%) when the
device was applied to changing target concentrations.
 Figure 12-14
Pharmacokinetic simulation demonstrating the limitations
of infusion regimens based on simple pharmacokinetic parameters, with fentanyl used
as an example. These infusion schemes were designed to achieve a plasma fentanyl
concentration of 3 ng/mL. The upper curve shows
that a regimen using a loading dose based on the volume of distribution followed
by a constant infusion based on clearance results in a transient period of extremely
high plasma concentrations. If the same maintenance infusion is given but the loading
dose is based on the volume of the central compartment, distribution of drug to the
peripheral compartments causes the plasma concentration to fall below the desired
level until the compartments reach steady-state concentrations, as shown in the lower
curve. Cp, plasma drug concentration.
Figure 12-14
Pharmacokinetic simulation demonstrating the limitations
of infusion regimens based on simple pharmacokinetic parameters, with fentanyl used
as an example. These infusion schemes were designed to achieve a plasma fentanyl
concentration of 3 ng/mL. The upper curve shows
that a regimen using a loading dose based on the volume of distribution followed
by a constant infusion based on clearance results in a transient period of extremely
high plasma concentrations. If the same maintenance infusion is given but the loading
dose is based on the volume of the central compartment, distribution of drug to the
peripheral compartments causes the plasma concentration to fall below the desired
level until the compartments reach steady-state concentrations, as shown in the lower
curve. Cp, plasma drug concentration.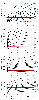 Figure 12-15
Nomogram for calculating maintenance infusion rates to
maintain a stable concentration of fentanyl, alfentanil, sufentanil, or propofol.
The y axis is the desired concentration. The x
axis is the time relative to the initial bolus. The diagonal
lines show the infusion rates at different times required to maintain
the desired concentration selected on the y axis.
Figure 12-15
Nomogram for calculating maintenance infusion rates to
maintain a stable concentration of fentanyl, alfentanil, sufentanil, or propofol.
The y axis is the desired concentration. The x
axis is the time relative to the initial bolus. The diagonal
lines show the infusion rates at different times required to maintain
the desired concentration selected on the y axis. Figure 12-16
Slide rule for calculating the maintenance propofol infusion
rate from the patient's weight, the desired target concentration, and the elapsed
time. (Adapted from Bruhn J, Bouillon TW, Ropcke H, Hoeft A: A manual slide
rule for target-controlled infusion of propofol: Development and evaluation. Anesth
Analg 96:142–147, 2003.)
Figure 12-16
Slide rule for calculating the maintenance propofol infusion
rate from the patient's weight, the desired target concentration, and the elapsed
time. (Adapted from Bruhn J, Bouillon TW, Ropcke H, Hoeft A: A manual slide
rule for target-controlled infusion of propofol: Development and evaluation. Anesth
Analg 96:142–147, 2003.)