|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
One objective of anesthetic administration is to produce the clinically desired time course of anesthetic effect, which usually includes rapid onset, smooth maintenance, and rapid recovery after termination of the anesthetic. Conventional pharmacokinetic models assume that a bolus of drug is instantaneously mixed into plasma and produces an immediate peak in the plasma concentration. The concentration then continuously declines until the next bolus. Except for a transient perioperative stimulus (intubation, incision, bowel traction), it is unlikely that the patient's anesthetic requirements follow the saltatory time course of anesthetic effect seen with repeated bolus injections. Thus, the technique of intermittent boluses results in excessive drug effect at the time of the bolus, inadequate drug effect before the next bolus, or both ( Fig. 12-2 ). The technique of giving the entire anesthetic as an initial bolus, as was popular in the early 1980s with massive doses of opioids for cardiac surgery, represents the reductio ad absurdum of the intermittent bolus technique. This technique produces a needlessly huge initial peak and, depending on the dose, grossly excessive or possibly subtherapeutic levels later in the procedure. Fortunately, opioids are enormously forgiving drugs in paralyzed patients whose lungs are mechanically ventilated.
The oscillating effect produced by intermittent bolus injection is particularly undesirable for drugs that depress hemodynamics or when prompt emergence is desirable. To produce a time course of drug effect that follows the time course of anesthetic requirement, it is necessary to use a
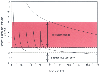 Figure 12-2
Pharmacokinetic simulation of (upper
curve) a single large bolus of fentanyl (50 µg/kg) and (lower
curve) a smaller fentanyl bolus (8 µg/kg) followed by intermittent
boluses (1.5 µg/kg) every 15 minutes. The single large bolus results in plasma
drug concentrations far in excess of those required, whereas the intermittent bolus
scheme results in plasma concentrations that periodically fall below the therapeutic
range. Ideally, the plasma drug concentration should be continuously within the
therapeutic range, which can best be accomplished by a continuous infusion.
Figure 12-2
Pharmacokinetic simulation of (upper
curve) a single large bolus of fentanyl (50 µg/kg) and (lower
curve) a smaller fentanyl bolus (8 µg/kg) followed by intermittent
boluses (1.5 µg/kg) every 15 minutes. The single large bolus results in plasma
drug concentrations far in excess of those required, whereas the intermittent bolus
scheme results in plasma concentrations that periodically fall below the therapeutic
range. Ideally, the plasma drug concentration should be continuously within the
therapeutic range, which can best be accomplished by a continuous infusion.
 Figure 12-3
Landscape of surgical anesthesia. The stimuli of surgery
are not constant; therefore, the plasma concentration of the anesthetic drug should
be titrated to match the needs of the patient.
Figure 12-3
Landscape of surgical anesthesia. The stimuli of surgery
are not constant; therefore, the plasma concentration of the anesthetic drug should
be titrated to match the needs of the patient.
The goal of intravenous administration is to produce plasma concentrations yielding the desired time course of drug effect. By the use of pharmacokinetic models, it is possible to calculate the dose of drug needed to produce the desired time course of plasma concentration. The medical literature is replete with articles describing pharmacokinetic models for every intravenous anesthetic drug. These models are of little use without computer simulation. In this chapter we will describe how pharmacokinetic models can be used to develop rational dosing
Pharmacokinetic models are mathematical descriptions of how the body "disposes" of drugs. The parameters describing this process are estimated by administering a known dose of the drug and measuring the resulting plasma concentrations. A mathematical model then relates the input over time, I(t), with the concentrations over time, C(t). These models can take many forms. Figure 12-4 shows the concentrations in plasma over time after a single intravenous bolus of drug at time 0. Drug concentrations continuously decrease after the bolus, and the rate of decrease is approximately proportional to the amount of drug in plasma. Typically, it is convenient to describe this behavior by the use of exponential models. The curve might have a single exponent, in which case the plasma concentration over time might be described by the function C(t) = A e−kt , where
 Figure 12-4
Steps involved in a pharmacokinetic model-driven infusion.
Typically, pharmacokinetic models are derived from experiments in which plasma drug
concentrations are measured at intervals after bolus administration of the drug.
Nonlinear regression is used to fit a monoexponential, biexponential, or triexponential
curve to the resulting concentration-versus-time data. There is an algebraic relationship
between the exponential decay curves and a one-, two-, or three-compartment pharmacokinetic
model. The "BET" infusion scheme is developed and consists of a bolus,
a continuous infusion to replace drug eliminated
from the body, and an exponentially declining infusion to replace drug transferred
out of plasma to other body compartments. A BET infusion results in maintenance
of a constant specified plasma drug concentration. Practical implementation of the
BET scheme with real infusion pumps and infusion rates that change only at discrete
intervals results in a plasma drug concentration profile that approximates the profile
resulting from a BET infusion.
Figure 12-4
Steps involved in a pharmacokinetic model-driven infusion.
Typically, pharmacokinetic models are derived from experiments in which plasma drug
concentrations are measured at intervals after bolus administration of the drug.
Nonlinear regression is used to fit a monoexponential, biexponential, or triexponential
curve to the resulting concentration-versus-time data. There is an algebraic relationship
between the exponential decay curves and a one-, two-, or three-compartment pharmacokinetic
model. The "BET" infusion scheme is developed and consists of a bolus,
a continuous infusion to replace drug eliminated
from the body, and an exponentially declining infusion to replace drug transferred
out of plasma to other body compartments. A BET infusion results in maintenance
of a constant specified plasma drug concentration. Practical implementation of the
BET scheme with real infusion pumps and infusion rates that change only at discrete
intervals results in a plasma drug concentration profile that approximates the profile
resulting from a BET infusion.
Intravenous anesthetic drugs may be administered by means other than single boluses. A more general way to think of pharmacokinetics is to decompose the input
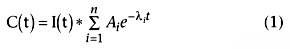
Pharmacokinetic modeling is the process of estimating the parameters within this function. The integer n is the number of exponentials (i.e., compartments) and is usually two or three for the drugs used in anesthesia. Each exponential term is associated with a coefficient Ai and an exponent λi . The λ values are inversely proportional to the half-lives (half-life = 0.693/λ), with the smallest λ value representing the longest (terminal) half-life. The A values are the relative contribution of each half-life to overall drug disposition. If a drug has a very long terminal half-life but a coefficient that is much smaller than the other coefficients, the long half-life is likely to be clinically meaningless. The * operator is the mathematical process called convolution, which can be thought of as multiplication, but for functions rather than for simple numbers. For a bolus at time 0, convolution is multiplication. For infusions, the math implied by the * gets more complicated, but the A and λ values estimated are the same.
Constructing pharmacokinetic models represents a trade-off between accurately describing the data, having confidence in the results, and achieving mathematical
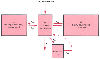 Figure 12-5
Three-compartment model (including the biophase) schematizing
the basic pharmacokinetic processes that occur after intravenous drug administration.
I, dosing scheme as a function of time; k10
,
rate constant reflecting all processes acting to irreversibly remove drug from the
central compartment; kij
intercompartmental
rate constants; V1
, central compartment volume, usually expressed in liters
or liters per kilogram.
Figure 12-5
Three-compartment model (including the biophase) schematizing
the basic pharmacokinetic processes that occur after intravenous drug administration.
I, dosing scheme as a function of time; k10
,
rate constant reflecting all processes acting to irreversibly remove drug from the
central compartment; kij
intercompartmental
rate constants; V1
, central compartment volume, usually expressed in liters
or liters per kilogram.
The pharmacokinetic model shown has some useful characteristics, thus accounting for its enduring popularity in pharmacokinetic analysis. Most importantly, the model describes observations from studies reasonably well, obviously the sine qua non for models. Second, these models have the useful characteristic of linearity. Simply stated, if you double the dose I (e.g., give a bolus twice as large or an infusion twice as fast), you double the concentration.
More generally, linearity implies that the system (i.e., the body acting to produce a plasma drug concentration output from a drug dosage input) behaves in accordance with the principle of superposition. The superposition principle states that the response of a linear system having multiple inputs can be computed by determining the response to each individual input and then summing the individual responses. In other words, when the body treats each bit of drug by polyexponential decay over time, that "disposing" of each bit of drug does not influence the disposing of other bits of drug.
The third reason for the continuing popularity of these models is that they can be mathematically transformed from the admittedly unintuitive exponential form shown earlier to a more easily intuitive compartmental form, as shown in Figure 12-5 . The fundamental parameters of the compartment model are the volumes of distribution (central, rapidly equilibrating, and slowly equilibrating peripheral volumes) and clearances (systemic, rapid, and slow intercompartmental). The central compartment (V1 ) represents a distribution volume and includes the rapidly
Despite their physiologic flavor, compartmental models are simply mathematical transformations of the polyexponential disposition functions computed from observed plasma concentrations. Thus, physiologic interpretation of volumes and clearances, with the possible exception of systemic clearance and VdSS (the algebraic sum of the volumes), is entirely speculative.
The last reason that these models have been popular is that they
can be used to design infusion regimens, which is the point of introducing them in
this chapter. If we abbreviate the disposition function

as simply D(t), we can rewrite the relationship between concentration, dose, and
the pharmacokinetic model D(t) as
C(t) = I(t) * D(t) (3)
where * is the convolution operator, as noted earlier. In the usual pharmacokinetic
study, we know I(t) (the dose we gave the patient), and we measure C(t), the concentrations
over time. Our goal is to find D(t), the pharmacokinetic disposition function.
Pharmacokinetic analysis can be thought of as a simple rearrangement of Equation
3 to solve for D(t):

where the symbol 
means deconvolution,
the inverse operation to convolution. Deconvolution is like division, but of functions
rather than simple numbers. When we design dosing regimens from known pharmacokinetic
models and a desired course for the plasma concentration over time, the known values
are D(t) (the pharmacokinetics) and CT
(t) (the desired target concentrations),
and the drug dosing scheme is

Thus, one can calculate the necessary infusion rates, I(t), given the desired target concentrations, CT (t), and the pharmacokinetics, D(t), by using the same tools used to calculate the original pharmacokinetics. Unfortunately, such a solution might require some negative infusion rates, which are obviously impossible. Because we cannot suck drug out of the body (i.e., give negative infusions), we must restrict ourselves to plasma concentrations over time that can be achieved with non-negative infusion rates.
The standard pharmacokinetic model has one glaring shortcoming. It assumes complete mixing within the central compartment after a bolus injection so that the peak concentration occurs precisely at time 0. It actually takes about 30 to 45 seconds for the drug to make its transit from the venous injection site to the arterial circulation. This model mis-specification of 30 to 45 seconds may not seem significant, but it can cause problems when one is trying to relate the drug effect after a bolus to drug concentrations in the body.[23] Researchers are modifying the standard polyexponential pharmacokinetic models to provide more accurate models of plasma drug concentration in the first minute after a bolus injection.[24]
|
|
|
|
|
|
|
|
|
|
|
|
|