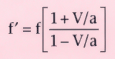APPENDIX 7: Ultrasound
The simplest sound wave to represent mathematically is a sinusoidal
wave propagating in one dimension:
p' = p0
sin [(2π/λ)(x − at)]
(1)
where p' is the pressure fluctuation, λ is the wavelength (distance between
waves), x is the coordinate in the direction of propagation,
and a is the speed of propagation, or the speed of
sound.
The amplitude of a sound wave is measured by the root mean square value of the pressure
fluctuations. This value is called the sound pressure level (SPL). Because the
range of SPL values is often very wide, a logarithmic scale is used:
SPL = 20 log (p*/P0
) (2)
where p* is the root mean square pressure fluctuation and P0
is a
reference pressure chosen as the lowest sound pressure detectable by the human ear.
This pressure representing the threshold of hearing is 2 × 10−8
kPa at a sound frequency of 2 kHz (2000 cycles/sec). The units in this
SPL scale are called decibels. Thus, a sound pressure of 2 × 10−8
kPa corresponds to an SPL of zero decibels (0 dB), the lowest audible
sound level [(p*/P0
= 1; log (1) = 0)].
Quiet conversation has an SPL of approximately 40 to 50 dB, or a pressure 10 to
300 times that of the threshold of hearing.
When sound waves encounter a sudden change in the properties of
the conducting medium, some of the sound is transmitted through the new medium, and
some of it is reflected, or "scattered," in many directions. Although the mathematics
of this process are complex, one conclusion is readily apparent: the greater the
mismatch in density and compressibility between the two media, the more sound that
is reflected. The quantity that best determines the degree of reflection at an interface
between two media is the ratio (R) of the products of density (ρ) and the speed
of sound (a) through the two media:
R = (ρ1
a1
)/(ρ2
a2
)
(3)
We can easily see that the greatest acoustic mismatch in the body occurs between
solid tissues and the lungs. Both the density and the speed of sound are much lower
in the air-filled lungs than in solid tissues. Therefore, ultrasonography cannot
"look" through the lungs at tissues or organs on the other side. The second greatest
mismatch occurs between soft tissues and bone, the latter having a much higher ρa
than the former. In 1842, Christian Johann Doppler first described the apparent
change in pitch of a sound that occurred when either the source of the sound or the
listener was moving. This Doppler effect now has several applications in patient
monitoring, including precordial and esophageal Doppler ultrasound devices that measure
local blood velocities or cardiac output. If a sound source radiating a frequency
(f) is stationary and the listener is moving (see Fig.
30-24A
), the wavelength of the waves can be determined by the equation
λ = a/f (4)
because the time between wave fronts is 1/f and the waves are moving at the speed
of sound (a). If the listener moves toward the source at speed V0
, the
velocity of the listener relative to the moving wave fronts is (a +
V0
). The number of wave fronts that the listener encounters
per unit time is therefore
f' = Velocity/Distance between waves = (a +
V0
)/λ (5)
Because the sound frequency for a stationary listener is f = a/λ
(Equation 4), the frequency f' heard by the moving listener becomes
f' = (a + V0
)/λ = f +
(V0
/λ) = f + (V0
f/a) = f[1 +
(V0
/a)] (6)
The apparent frequency of the listener is thus increased by the factor [1
+ (V0
/a)]. A listener moving toward the source at half
the speed of sound hears a frequency 1.5 times that of a stationary listener.
Now consider a stationary listener and a source moving at speed
V0
, as shown in Figure
30-24B
. The wave fronts are no longer concentric circles; they are more
closely spaced in the direction that the source is moving. If the frequency of the
sound emitted at the source is f, the source moves a distance V0
/f during
each vibration. The wavelength in the direction of motion is thus shortened by V0
/f
and becomes 1 = (a − V0
)/f. The waves
themselves are traveling at speed a, so the frequency heard by the stationary listener
is
f' = a/λ' = af/(a − V0
)
= f[1/(1 − V0
/a)] (7)
Now, if the source is moving at half the speed of sound toward the listener, the
apparent frequency doubles. Compare this situation with the preceding one in which
the listener is moving and the apparent frequency increases by only 50%. Doppler
ultrasound systems combine the two situations shown in Figure
30-24
. The initial acoustic source is a stationary transducer, and the
sound from this device is scattered from a moving target (e.g., red blood cells).
The scattered sound then returns to a stationary listener: the receiving transducer.
In effect, the target is a moving listener hearing a stationary source; the target
then reradiates the sound as a moving source toward a stationary listener. The frequency
heard by the receiving transducer is obtained by combining Equations 6 and 7:
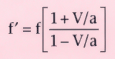
In this example we have assumed that the target is moving toward the ultrasound transducers
at speed V. If the target is moving at half the speed of sound, the observed frequency
is increased by a factor of 3! Because changes in the frequency of sine waves can
be measured precisely, the Doppler principle provides a very accurate method of measuring
the velocity of moving sound reflectors. At the high frequencies often used (≥5
MHz), objects as small as red corpuscles can scatter enough sound for detection.
Ultrasound imaging is exceptionally complex. For simplicity's
sake, recall the submarine movies wherein the sonar operator calls out "range 2000
yards, bearing 36 degrees." These two parameters are critical in describing some
of the math of ultrasound.
The first factor to consider is the maximal range of the ultrasound,
which is described by the following relationship:
rmax
= cT/2
That is, the maximal range equals the speed of sound in tissue (≅1540 m/sec) multiplied
by the time T between pulses divided by 2. A further limitation is the fact that
the energy dissipates in the tissue. (You need to tap harder when percussing to
detect deeper structures). For deeper penetration into tissues, one requires higher
energies and slower pulse rates. Wavelength and frequency are related in the following
manner:
λ = c/f
where f is the frequency, λ is the wavelength, and c is the speed of sound.
Next we need to consider both the axial resolution (is the enemy
destroyer 2000 yards distant, or 2005?) and the annular resolution (is the bearing
36 or 38 degrees?). Sound in tissue spreads out in a bandwidth around a fundamental
frequency. So to determine the necessary bandwidth for an axial resolution of 2
mm, the following rough approximation holds:
B = 2c/Δr
where Δr is the axial resolution. Therefore we need a bandwidth of 1.54 MHz
to get an axial resolution of 2 mm.
For annular resolution (Δtheta), remember that the beam
spreads out the further it goes from the source. Without deriving the mathematics,
two factors determine annular resolution, the frequency and the aperture. Aperture
size is limited to a size that will fit into or onto a human. Remember that a 1-degree
error at a 1-cm range will increase at a 10-cm range: circumference = 2πr: 1/360
× 2 × π × 1 = 0.17 mm; thus, at 10 cm, circumference
= 1.7 mm.