BASIC PRINCIPLES

Nature of Physics and Measurement

What is monitoring? The verb monitor (derived from the Latin monere, "to warn") means to check systematically or to keep watch over. In the context of anesthesiology, monitoring means using both our senses and electronic devices to repeatedly or continuously measure important variables in an anesthetized patient.

Physics is the science of matter and energy and interactions between the two; that is, it is the study of everything in the physical universe. Physics encompasses everything from the motions and inner workings of the atom to those of galaxies. Physics is quantitative, and mathematics is the language of physics. In fact, Isaac Newton invented "the calculus" as a tool for expressing and studying the laws of physics. Our monitors are also quantitative. Before we can discuss and understand the complexity of modern anesthetic monitors, we must quantitatively define what we are attempting to measure.

We measure and monitor mass and energy: how much of a substance is present and in what energy state. Much of what we desire to monitor is outside the range of human physical senses. Therefore, we must make measurements in this insensible realm with devices that enhance or extend our senses. Just as the senses have limitations and can be "fooled" under certain circumstances ( Fig. 30-1 ), our physiologic monitors are limited by their design and can also be fooled under some conditions. Intelligent users of these devices must understand their basic design assumptions to predict when they are likely to produce erroneous data.

As we make measurements of mass, space, time, and other physical variables, we often encounter confusion between the terms units and dimensions. A dimension describes the measure by which a physical variable is expressed quantitatively. For example, length (1) is the dimension used to describe distance, height, or width. Units are specific ways of measuring a given dimension: meters, feet, furlongs, and light-years are all units of length. In basic mechanics, all dimensions can be expressed in terms of the three fundamental dimensions of mass (m), length (l), and time (t). In problems of energy transport, an additional dimension of temperature or heat content must be added. In electricity and magnetism, the dimension of charge is also required.

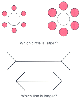Figure 30-1 Optical illusions. We perceive the circles to be different sizes because we infer the size by relative dimensions. The closeness of the smaller circles makes the inner circle appear smaller, and vice versa. The lines appear to be different sizes because we use straight-line perspective to estimate size and distance. This illusion reportedly does not work in cultures where straight lines are not used. Therefore, our internal perceptions lead us to err in estimating size and length. In the same way, the internal programming of our monitors can lead us to misinterpret results.

As stated earlier, units are specific ways of measuring a particular dimension. Although there are many units of mass, length, and time, the scientific community has standardized to the Systeme International d'Unites, or SI units: length in meters, mass in kilograms, time in seconds. To understand how all quantities in basic mechanics can be expressed in terms of mass (m), length (l), and time (t), we must introduce one (and only one) equation: Newton's second law of motion, the basis of all classic physics:

F = ma (1)

Stated in English, force equals mass times acceleration. Force and acceleration are vectors; that is, they have both magnitude and direction. Mass is a scalar; it has only magnitude. From this simple equation we can see that the dimensions of force must be the dimensions of mass times those of acceleration. Acceleration is the rate of change in velocity, and velocity is the rate of change in distance. Thus, velocity has dimensions of length divided by time, l/t, and acceleration has dimensions of l/t/t, or l/t² . The SI units of acceleration are meters per second per second, or m/sec² . Because the SI unit of mass is the kilogram, Equation 1 tells us that the unit of force must be kg-m/s² (kilogram-meters per second squared). This unit is called the newton, after Sir Isaac, so 1 N = 1 kg-m/s² .

Other dimensions and units can be derived in the same way. For example, kinetic energy is proportional to mass times velocity squared (mv² ), so its dimensions are m(l/t)² , and its SI unit is kg-m² /sec² . Because "kilogrammeter squared per second squared" is quite a mouthful,

1193

Measurement is the determination of a physical quantity (e.g., mass, length, time, energy, and any of their derivatives). Measuring depends on a physical interaction. If a mass or energy does not interact with anything, it cannot be perceived to exist. As we have stated, physics uses the second, meter, and kilogram to measure time, space, and matter. How do we define the size of these standard units? Historically, the second was defined as a fraction (1/60 of 1/60 of 1/24) of a day. However, because of tidal forces on the earth, the days are becoming longer, and the second is now defined as the interval required for 9,192,631,770 vibrations of the cesium 133 atom measured via an atomic beam clock. The meter was originally one ten millionth of the distance from the North Pole to the Equator. In 1960, the meter was redefined to be 1,650,763.73 wavelengths of orange-red light from a krypton 86 lamp. Today, the meter is defined as the distance that light travels in a vacuum during a time of 1/299, 792,458 second because time can be measured with better accuracy and precision than the wavelengths of a krypton lamp. The gram was originally defined as the weight of the volume of pure water at 4°C that occupies a cube that is one hundredth of a meter on all sides. Today, the kilogram is defined as a unit of mass based on a physical standard (a platinum-iridium cylinder).

Temperature is related to the energy per unit mass of a substance in the form of motion on an atomic level. When an object of higher temperature is brought into contact with one of lower temperature, thermal energy, or heat, spontaneously passes from the "hot" to the "cold" object until the two reach equilibrium at a temperature between the two original temperatures. In gases, temperature is a quantitative measure of the kinetic energy of molecular motion per unit mass. In 1742, Celsius proposed a temperature scale of degrees with the freezing point of water used as 0°C and the boiling point of water at 1-atm pressure used as 100°C. A temperature of absolute zero is defined as the point at which the molecules in a substance are in their lowest possible energy state. This condition occurs at -273.15°C or, in SI units, 0° Kelvin (K).

Physical measurements can be either continuous or discrete. That is, we can measure a distance of 3.1416 m, but we cannot measure out 3.1416 eggs. We consider most numerically defined quantities to be continuous. However, when we measure very tiny quantities (wavelengths of light, energies of photons, masses of atoms), we find that our measurements are not continuous; they change in small jumps, or quanta. Continuous measurement is thus an illusion, but a practical one for most purposes.