PREOPERATIVE AND PREPROCEDURE TESTING
Most hospitals, many anesthesia departments, many outpatient surgical
centers, and now many office-based operatories have rather arbitrary rules and recommendations
regarding tests that should be performed before elective surgery. With good intentions,
anesthesiologists tried to follow those rules, and problems began. The inexpensive
multiphasic screening batteries of tests subsequently developed by the Kaiser Hospitals
and Health Plan seemed to be the answer to this confusing and arbitrary process.
[170]
Physicians believed they could now order
inexpensive
batteries of tests and thus efficiently screen for disease. However, physicians
were still trying to determine which tests to order before surgery, and what to do
with the unexpectedly abnormal result on the morning of surgery. Kaiser found that
this system of preoperative multiphasic screening was not practical.[171]
The system produced so many false-positive and false-negative results that the subsequent
harm vastly outweighed any possible benefit. Nevertheless, the notion of "the more
testing, the better" is still with us.
The Low Predictive Value of an "Abnormal" Laboratory
Test Result
Understanding what constitutes an "abnormal" laboratory test result
requires an appreciation of the way "normal" values are determined. A normal range
is based on the typical distribution of the gaussian curve.[172]
For example, assuming a gaussian distribution and hemoglobin values of 13.5 to 16.7
g/dL ("reference range") for healthy men, one can expect 5% of "normal" men to have
a test result outside that range.
Of prime importance in preoperative evaluation is knowing the
percentage of abnormal laboratory test values that truly indicates disease. If the
anesthetic management of a patient is altered because of a test abnormality, that
abnormality should indicate a condition (1) that poses a significant risk of preoperative
morbidity that can be lessened by preoperative treatment, (2) that cannot be discovered
through history-taking and physical examination, and (3) that is sufficiently prevalent
in the population to justify the risk of performing the follow-up test. To be cost-efficient,
the test should be sufficiently "sensitive" (have "positivity in disease") and sufficiently
"specific" (have "negativity in health"). That is, test results should be positive
if the patient has disease and negative if the patient is healthy.[172]
[173]
[174]
In
fact,
what a clinician really wants to know is what a positive or negative test means for
the individual patient in front of him or her. The values representing the predictive
ability of a positive or negative test ("positive predictive values" and "negative
predictive values") depend on the pretest population probability.[172]
[173]
[174]
We shall now consider the significance of false-positive and false-negative
results and the prevalence of disease in the test population in relation to abnormal
laboratory test results. (I am indebted to Drs. Jorgen Hilden and Anders Hald, whose
comments have helped make this section clearer.) For example, patients with pneumonia
would have the notation "pneumonia" (or some significant abnormality) written as
the diagnosis on their chest radiograph reports. Let us assume that the specificity
of a test (its negativity in health) is 98.3%; that is, 983 of 1,000 people who actually
do not have asymptomatic pneumonia will have a comment such as "without evidence
of pneumonia" or "normal" written on their chest radiograph reports. Next, let us
assume that 0.5% of the asymptomatic population under age 40 who are about to undergo
routine elective surgery has pneumonia. Given the preceding assumptions, what is
the likelihood that a person whose chest radiograph report reads "pneumonia" would
actually have pneumonia?
If we test 100,000 asymptomatic persons, and 0.5% are assumed
to be diseased, this means that 500 people would have undetected pneumonia. If the
sensitivity of chest radiographs to pneumonia is assumed to be 75%, 375 of these
people would have abnormal radiographs. Then, if specificity is assumed to be 98.3%,
97,809 of the 99,500 healthy people would have normal results on chest radiographs.
This means that 1,691 (1.7%) would have abnormal radiographic results. Thus, of
2,066 patients having a diagnosis of pneumonia based on chest radiographs, 1,691
(82%) of the results would be falsely positive. Therefore, it is entirely possible
that 82% of the chest radiographs indicating "infiltrate compatible with pneumonia"
in otherwise asymptomatic persons would actually be radiographs of totally healthy
people. Expressed in another way, when the above assumptions discussed are applied,
the likelihood that an asymptomatic person would actually have pneumonia when the
chest radiograph contains that notation is only 18%; that is, for this patient group,
the predictive value of a positive test (the "positive predictive value") is only
18%.
Only patients with abnormal test results who actually have disease
("true positives") benefit from laboratory testing. Let us assume that 2.2% of the
chest radiographs in the under-age-40 population are positive, and that, for each
true positive, perioperative mortality decreases by 50%. If we use the 82% false-positive
rate derived previously, the number of patients benefiting per 1,000 radiographs
is 3.9 (true positives per 1,000 = all positives − false positives;
i.e., [2.2% × 1,000] − [82% percent − 2.2 percent ×
1,000] = 3.9 patients). Therefore, a reduction in operative mortality
of 50%, or 1 per 20,000 (i.e., 3.9 − 0.5 × 0.00005),
gives 0.000095 fewer deaths per 1,000 operations when preoperative chest radiographs
are obtained.
Hilden and Hald (personal communication) question whether this
is a logical calculation. For example, one study analyzed outcomes for asymptomatic
patients.[175]
The death rate for this group was
1 in 10,000. Of these deaths, more than 90% were caused by avoidable problems unrelated
to unknown diseases. Therefore, at most, fewer than 10% of the deaths of asymptomatic
individuals could be attributed to preoperative conditions, and probably fewer than
10% of those deaths (<1% of the total, or 1 in 1,000,000) would be related to
pneumonia. Thus, the intuitive value is similar to what we have estimated. Furthermore,
from an examination of the data in Table
25-5
and Table 25-10
,
it is evident that few chest radiographs in the under-40 asymptomatic population
led to benefit. In addition, the harm from these tests has not yet been considered.
Translating this figure into the present value for years of life
saved per 1,000 chest radiographs yields the following: 0.000095 fewer
deaths per 1,000 operations × 22.62 years saved per life saved = 0.0022
years of life (22.62 is the present value of 60 more years of life for
a 20-year-old, per Neuhauser[172]
). At the University
of Chicago, the 0.0022 years of life saved would cost $78,000 (an anteroposterior
and lateral chest radiograph cost $78, not including fees for consultations, repeated
radiographs, or other laboratory tests or procedures). Therefore, each year of life
saved by
TABLE 25-10 -- Screening chest radiographs: Incidence of abnormal test results, the discovery
of which may change management of anesthesia
|
Age(y) |
Series |
Patients Examined
(n) |
Abnormalities
*
(%) |
New Abnormalities
†
(%) |
|
0–14 |
Farnsworth et al[176]
|
350 |
8.9 |
0.3 |
|
0–18 |
Brill et al[177]
|
1,000 |
1.9 |
0.7 |
|
0–19 |
Sagel et al[178]
|
521 |
0 |
0 |
|
0–19 |
Sane et al[179]
|
1,500 |
5.4 |
2.2 |
|
0–19 |
Wood and Hoekelman |
749 |
4.7 |
1.2 |
|
1–20 |
Rees et al[180]
|
46 |
0 |
0 |
|
20–29 |
Sagel et al[178]
|
894 |
1 |
— |
|
21–30 |
Rees et al[180]
|
62 |
3 |
— |
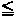 30 30 |
Loder[181]
|
437 |
10.1 |
0.2 |
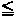 30 30 |
Hubbell et al[182]
|
12 |
0 |
0 |
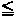 30 30 |
Maigaard et al[183]
|
1,256 |
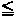 4.5 4.5 |
0 |
|
0–39 |
Umbach et al[166]
|
305 |
3.0 |
— |
|
30–39 |
Sagel et al[178]
|
942 |
2.3 |
— |
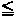 40 40 |
Catchlove et al[184]
|
29 |
0 |
0 |
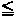 40 40 |
Collen et al[170]
|
15,978 |
2.1 |
— |
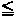 40 40 |
Sagel et al[178]
|
2,357 |
1.3 |
1.3 |
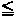 40 40 |
McKee and Scott[112]
,
‡
|
26 |
7.7 |
3.9 |
 40 40 |
Combined[112]
[176]
[177]
[178]
[179]
[181]
[182]
[183]
,
§
|
6,787 |
4.0 |
0.8 |
|
40–49 |
Sagel et al[178]
|
928 |
7.1 |
|
|
<40 |
Velanovich[185]
|
— |
3.1 |
— |
|
40–49 |
Umbach et al[166]
|
290 |
6.2 |
— |
|
40–59 |
Collen et al[170]
|
21,489 |
7.4 |
— |
|
41–50 |
Hubbell et al[182]
|
28 |
17.9 |
0 |
|
41–50 |
Rees et al[180]
|
119 |
19 |
— |
|
41–50 |
McKee and Scott[112]
,
‡
|
53 |
17 |
0 |
|
30–69 |
Loder[181]
|
515 |
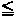 6.0 6.0 |
— |
|
31–40 |
Rees et al[180]
|
93 |
13 |
— |
|
31–40 |
Hubbell et al[182]
|
22 |
22.5 |
4.5 |
|
40–60 |
Velanovich[185]
|
NA |
23.9 |
— |
|
≧40 |
Sagel et al[178]
|
3,689 |
23.9 |
6.0 |
|
≧40 |
Catchlove et al[184]
|
50 |
0 |
0 |
|
≧40 |
Thomsen et al[186]
|
1,823 |
2.3 |
0.2 |
|
50–59 |
Umbach et al[166]
|
247 |
10.9 |
— |
|
50–59 |
Sagel et al[178]
|
733 |
20.3 |
— |
|
51–60 |
Hubbell et al[182]
|
87 |
36.8 |
4.4 |
|
51–60 |
Rees et al[180]
|
121 |
40.0 |
— |
|
51–60 |
McKee and Scott[112]
,
‡
|
85 |
40.0 |
0 |
|
>55 |
Gupta et al[187]
,
‡
|
346 |
5.5 |
0.9 |
|
60–69 |
Umbach et al[166]
|
202 |
13.3 |
— |
|
60–69 |
Sagel et al[178]
|
977 |
29.7 |
— |
|
61–70 |
Boghosian and Mooradian[188]
|
78 |
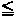 49 49 |
— |
|
>60 |
Boghosian and Mooradian[188]
|
|
|
|
|
Without risk factor
‡
|
44 |
34.0 |
— |
|
With risk factors |
92 |
62.0 |
— |
|
>60 |
Collen et al[170]
|
7,196 |
19.2 |
— |
|
>60 |
Hubbell et al[182]
|
145 |
44.1 |
4.8
‖
|
|
>60 |
McKee and Scott[112]
,
‡
|
163 |
44.2 |
1.9 |
|
>60 |
Velanovich[185]
|
NA |
31.9 |
— |
|
61–70 |
Rees et al[180]
|
134 |
43.3 |
— |
|
61–70 |
Hubbell et al[182]
|
94 |
36.2 |
5.4 |
|
>65 |
Sewell et al[189]
|
28 |
21 |
— |
|
≧69 |
Loder[181]
|
48 |
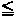 72.9 72.9 |
— |
|
≧?70 |
Wolf-Klein et al[137]
|
500 |
1.9 |
— |
|
≧70 |
Sagel et al[178]
|
832 |
41.7 |
— |
|
≧70 |
Törnebrandt and Fletcher[180]
|
100 |
37 |
8.1? |
|
≧70 |
Boghosian and Mooradian[188]
|
|
|
|
|
Without risk factors
‡
|
58 |
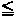 59 59 |
— |
|
With risk factors |
45 |
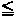 64 64 |
— |
|
≥71 |
Levinstein et al[156]
|
121 |
84.4 |
0.9 |
|
70–79 |
Umbach et al[166]
|
110 |
27.2 |
— |
|
71–80 |
Rees et al[180]
|
76 |
61.8 |
— |
|
71–80 |
Hubbell et al[182]
|
28 |
57.1 |
0 |
|
>80 |
Umbach et al[166]
|
21 |
33.3 |
— |
|
>80 |
Hubbell et al[182]
|
23 |
60.9 |
8.7 |
|
20–89 |
Fink et al[191]
|
127 |
46 |
— |
|
74–97 |
Domoto et al[136]
|
69 |
72.5 |
33 |
|
>81 |
Rees et al[180]
|
16 |
68.8 |
— |
|
?0–?90 |
Wiencek et al[192]
|
403 |
≤25.1 |
2.4 |
|
0–90 |
Delahunt and Turnbull[139]
|
860 |
— |
0 |
|
24–90 |
Tape and Mushlin[149]
,
¶
|
318 |
33 |
0 |
|
0–?90 |
Petterson and Janower[193]
|
1,530 |
9.8 |
1.3 |
|
0–?90 |
Turnbull and Buck[113]
,
¶
|
691 |
5.5 |
— |
|
0–?90 |
Royal College[184]
|
3,052 |
3.8 |
— |
|
0–?90 |
Rucker et al[195]
,
‡
|
371 |
0.3 |
— |
|
0–?90 |
Blery et al[128]
|
2,765 |
0.7 |
0.1 |
|
0–90+ |
Weibman et al[196]
,
¶
|
734 |
5.0 |
— |
|
0–90+ |
Muskett and McGreevy[115]
|
119 |
29.4 |
5.0 |
|
0–90+ |
Gagner and Chiasson[197]
|
1,000 |
7.4 |
— |
*These
data constitute an edited summary of the data presented by various articles, edited
to select abnormalities that might change management of anesthesia.
†Abnormalities
not already known or suspected by history or physical examination.
‡Patients
were asymptomatic.
§Combined studies in younger-than-40
population excluding two studies, those by Rees et al[180]
and Collen et al.[170]
‖0% changed
treatment.
¶Tape
and Mushlin[149]
studied vascular surgery patients;
Turnbull and Buck,[113]
cholecystectomy patients;
and Weibman and colleagues,[196]
cancer patients.
obtaining chest radiographs costs about $35,500,000 (78,000 divided by 0.0022).
However, just as there are other costs (e.g., pursuing some false-positive
chest shadows will result in computed tomographic needle biopsies and lobectomies
in totally healthy patients[109]
[110]
[111]
[112]
), there
are other benefits (e.g., treatment of some patients having solitary nodules or mediastinal
masses may prolong life). Let us arbitrarily assume that these costs and benefits
are equal. One is forced to conclude that screening for an asymptomatic disease
having a low prevalence rate is a very expensive and possibly risky procedure.