Previous Next

Stewart-Fencl Approach

A more accurate reflection of true acid-base status can be derived using the Stewart-Fencl approach.[1] [2] This is based on the concept of electrical neutrality, a small advance from using the AG. There exists in plasma a SID of [(Na+ + Mg2+ + Ca2+ = K+ ) − (Cl− + A− )] of 40 to 44m Eq/L, balanced by the negative charge on bicarbonate and ATOT (the buffer base). There is a small difference between SIDa (apparent SID) and buffer base (effective SID [SIDe]). This represents a strong ion gap (SIG), which quantifies the amount of unmeasured anions present ( Fig. 41-5 ).

SIDa = ([Na+ ] + [K+ ] + [Mg2+ ] + [Ca2+ ]) − [Cl− ]

SIDe = [HCO3 − ] + (charge on albumin) + (charge on inorganic phosphate [Pi]) (in mmol/L)

Weak acids' degree of ionization is pH dependent, and calculations must include this:

[alb] = [alb] (in g/L) × (0.123 × pH − 0.631)

[Pi] (in mg/dL) = [Pi] / 10 × pH − 0.47.

SIG = SIDa − SIDe

The weakness of this system is that the SIG does not necessarily represent unmeasured strong anions but merely


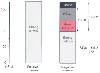Figure 41-5 The strong ion gap apparent (SIDa) is the sum of the total concentration of weak ions (ATOT ), such as albumin (Alb) and inorganic phosphate (Pi), plus the concentration of bicarbonate ions [HCO3 - ]. SID effective (SIDe) is the real SID. The difference between the two is made up of unmeasured anions (UMAs).

all anions that are unmeasured. SID changes quantitatively in absolute and relative terms when there are changes in plasma water concentration. Fencl addressed this problem by correcting the chloride concentration for free water, [Cl- ] corrected with the following equation:

[Cl− ]corrected = [Cl− ]observed × ([Na+ ]normal/[Na+ ]observed)

This corrected chloride concentration may be then inserted into the previous SIDa equation. Likewise, the derived value for UMAs should also be corrected for free water using UMAs instead of Cl- in the previous equation.[18] In a series of nine normal subjects, Fencl estimated the normal SIG as 8 ± 2 mEq/L.[18]

Although accurate, the SIG is cumbersome and expensive, requiring measurement of multiple ions and albumin. An alternative approach, used by Gilfix and colleagues[31] and subsequently by Balasubramanyan and coworkers,[32] is to calculate the BD or base excess gap (BEG). This allows recalculation of BDE using strong ions, free water, and albumin. The resulting BEG (i.e., BE caused by UMAs) should mirror the SIG and AG, and these terms may be manipulated to provide the following equations and definitions:

BEG = BDE − CBE

BDE = Standard BDE

CBE = Calculated BDE

BEfw = Changes in free water = 0.3 × (Na − 140)

BECl = Changes in chloride = 102 − (Cl − 140/Na)

BEalb = Changes in albumin = 3.4 × (4.5 − albumin)

CBE = BEfw + BECl + BEalb

It is probable that no single number will ever allow us to make sense of complex acid-base disturbances. Fencl[18] has suggested that, rather than focusing on AG or BDE, physicians should address each blood gas in terms of all alkalinizing and acidifying effects: respiratory acidosis or alkalosis, the presence or absence of abnormal SID (due to water excess or deficit, measured electrolytes or unmeasured electrolytes), and abnormal ATOT . This does not necessarily mean that when examining a blood gas result and serum chemistry profile, the physician is required to perform a series of calculations. Many acid-base abnormalities can be inferred by "eyeballing" the laboratory values[18] :

  1. Hyperchloremic acidemia is usually present if the corrected serum chloride level is more than 112 mEq/L.
  2. Hypochloremic alkalemia is usually present when the corrected serum chloride level is less than 100 mEq/L.
  3. Dilutional acidemia is usually present when the serum sodium level is less than 136 mEq/L.
  4. Contraction alkalemia is usually present when the serum sodium level is more than 148 mEq/L.
  5. Hyperphosphatemic acidemia is usually present when the serum phosphate level is more than 2.0 mmol/L.
  6. Hypoalbuminemic alkalosis is usually present when the serum albumin level is less than 3.5 g/dL.

Although this approach may appear inelegant, it has the advantage of being comprehensive. Consider the following data for a patient described by Fencl [18] (in mEq/L unless

1609
otherwise stated): Na = 117, K = 3.9, Ca = 3.0, Mg = 1.4, Cl = 92, Pi = 0.6 mmol/L, albumin = 6.0 g/L, pH = 7.33, PCO2 = 30 mm Hg, HCO3 = 15, AG = 13, AGcorrected = 23, BE = -10, SID = 18, Clcorrected = 112, and UMAcorrected = 18. Using traditional methodology, this would be described as a non-AG metabolic acidosis, and the physician would look for causes of bicarbonate wasting, such as renal tubular acidosis or gastrointestinal losses. The degree of respiratory alkalosis is appropriate for the degree of acidosis (ΔBD = ΔPCO2 ). However, the Fencl-Stewart method reveals a much more complex situation. SID is reduced to 18 mEq/L, caused by free water excess, UMAs, and surprisingly, hyperchloremia (see the corrected chloride value). However, the degree of acidosis does not mirror this metabolic disturbance because of the alkalizing force at play: hypoalbuminemia. The corrected AG mirrors the change in SID, but this is grossly underestimated by the BD. This patient has a dilutional acidosis, a hyperchloremic acidosis, and a lactic acidosis!

For most patients presenting to the emergency room or operating suite who have been previously healthy, the use of tools such as the BD or AG to assess metabolic disturbances remains reasonable. However, for critically ill patients, the most effective method of interpreting acid-base conundrums involves unraveling synchronous acidifying and alkalinizing processes and using calculations or rules of thumb to distinguish between the various forces at play. Unfortunately, a clinician's ability to interpret such information depends on the amount of available data. A simple blood gas determination alone may camouflage a significant acid-base disturbance.

Previous Next