Base Deficit or Excess (Copenhagen) Approach
Singer and Hastings[24]
pioneered
an alternative approach to acid-base chemistry in 1948, by moving away from the Henderson-Hasselbalch
description toward quantifying the metabolic component. They proposed that the whole
blood buffer base (BB) could be used for this purpose. The buffer base represented
the sum of the bicarbonate and the nonvolatile buffer ions (essentially the serum
albumin, phosphate, and hemoglobin). Applying the law of electrical neutrality,
the buffer base was forced to equal the electrical charge difference between strong
(fully dissociated) ions. Normally, BB = [Na+
]
+ [K+
] − [Cl−
]. Alterations
in buffer base essentially represented changes in strong ion concentrations (which
could not be easily measured in 1948), buffer base increases in metabolic alkalosis,
and decreases in metabolic acidosis. The major drawback of the use of buffer base
measurements is the potential for changes in buffering capacity associated with alterations
in hemoglobin concentration.
In 1958, Siggard-Anderson and colleagues[24A]
developed a simpler measure of metabolic acid-base activity, the BDE (base deficit
or excess). They defined the BDE as the amount of strong acid or base required to
return pH to 7.4, assuming a PCO2
of 40
mm Hg and temperature of 38°C. The initial use of whole blood base excess was
criticized because of the dynamic activity of red blood cells within the acid-base
paradigm of gas and electrolyte exchange. This approach was modified in the 1960s
to use only serum base excess (BE), and the calculation became the standardized
base excess (SBE). Like the Boston group, their data were based on observations
of a large population of patients, leading to the development of nomograms ( Fig.
41-3
and see Table 41-3
).
Current algorithms for computing the SBE are derived from the Van Slyke equation
(1977).[25]
The BDE approach to acid-base chemistry
has been successfully validated by Schlitig[26]
and Morgan.[27]
The SBE is computed by blood gas analyzers by using the following
equation:
SBE = 0.9287 × [HCO3
−
− 24.4 + (pH − 7.4)].
Simple mathematical rules can be applied using the BDE in each of the common acid-base
disturbances. For example,
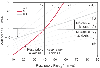Figure 41-3
Acid-base nomogram using the Copenhagen approach as revised
by Schlichtig. The various acid-base disturbances can be distinguished based on
PCO2
and base deficit or excess, here
referred to as standard base excess (SBE). Arrows
represent changes as the body compensates for acute acidosis or alkalosis. AR, acute
respiratory acidosis or alkalosis; CR, chronic respiratory acidosis or alkalosis;
M, metabolic acidosis or alkalosis. (From Schlichtig R, Grogono AW, Severinghaus
JW: Human PaCO2
and standard base excess
compensation for acid-base imbalance. Crit Care Med 26: 1173–1179, 1998.)
in acute respiratory acidosis or alkalosis, BDE does not change. Conversely, in
acute metabolic acidosis, the magnitude of change of the PCO2
(in millimeters of mercury) is the same as that of the BDE (in milliequivalents per
liter) ( Table 41-3
).
There has been considerable discussion over the past 30 years
about the merits and demerits of the BDE compared with the CO2
-HCO3
-
system. In reality, there is little difference between the two; both equations and
nomograms were derived from in vivo patient data and abstracted backward. Consequently,
for most patients, either approach is relatively accurate but misleading. Using
measures of buffer base as a means of quantifying acid-base disturbances, these techniques
do not allow the clinician to distinguish between, for example, acidosis
due to lactate or chloride, or alkalosis due to dehydration or hypoalbuminemia.
These measures may miss the presence of an acid-base disturbance entirely; for example
a hypoalbuminemic (metabolic alkalosis), critically ill patient with a lactic acidosis
may have a normal range pH, bicarbonate, and BE. This may lead to inappropriate
therapy.
